A Mathematical Model of Tritrophic Systems
- DOI
- 10.2991/jrnal.k.211108.002How to use a DOI?
- Keywords
- Chemical ecology; Lotoka–Volterra equation; tri-trophic system; mathematical biology
- Abstract
Lotoka–Volterra, LV equations are to model predator–prey problem. In principle, the LV equations are belongs to a two-person system. Even if there are many-body, it is structurally in two-body, i.e., with three or more predators and a prey. On the other hand, chemical ecology has shown that plants damaged by predation produce information chemicals (Hervibore Induced Plant Volatile, HIPV) that attract natural enemies. Chemical ecology suggests that the ecosystem is a tri-trophic system consisting of predator–plant (HIPV)–prey. Therefore, chemical ecosystems are essentially different from LV equations. This paper proposes a basic equation for tri-trophic systems and investigates their stability.
- Copyright
- © 2021 The Author. Published by Atlantis Press International B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Mathematical ecology has used the Lotoka–Volterra, i.e., LV equations which are the basic equation of the theory [1]. LV equations are differential equations with the predator as y and the prey as x, shown in Equations (1) and (2).
The equilibrium point of the LV equation can be found as the point where the derivative of x and y is zero; as shown in Equations (3) and (4);
We obtain the equilibrium points,
The positive and negative differential values of x or y around equilibrium points give the behavior of the LV equations.
If y is more significant than k1/k2, x decreases, and if y is minor, it increases. On the other hand, if x is more prominent than k3/k2, y increases, and if it is smaller, y decreases. Therefore, x and y oscillate around the equilibrium point; the solution to these equations are periodic (Figure 1) [1].

Dynamics of LV equation.
1.1. Chemical Ecology
The LV equations do not include plants. Therefore, the LV equations can also describe carnivores–herbivores relationships other than herbivores and carnivores [2].
Since the late of 1980s, chemicals are essential to ecosystems. Animals, insects, and plants produce non-volatile chemicals and volatile chemicals such as proteins. Non-volatile chemicals are used, for example, for individual recognition between insects; personal credit is done by touching proteins on the body surface of the other insect with the antennae. On the other hand, Volatile chemicals are Terpenes produced by plants; the Terpenes are called Herbivores Induced Plant Volatile, HIPV [3,4]. Terpene is a hydrocarbon composed of isoprene, a biological substance produced by plants, insects, and fungi.
When a plant is attacked, the plant chemically analyzes the saliva of the attacker and identify it. A plant can identify multiple attackers by its saliva. If the plant tells the attacker, it produces a volatile chemical that attracts the attacker’s natural enemies. About three types of terpenes are used in the interaction between natural enemies and plants. Different blends of these terpenes are used to attract suitable natural enemies.
In the case plants suffer mechanical damage, they synthesize salicylic acid to repair the damage. On the other hand, when attackers damage a plant, the plant switching synthesizing salicylic acid to terpenes.
2. MODEL OF TRI-TROPHIC SYSTEM
2.1. Rule Dynamics
The group dynamics governing the elements can exist in a variety of forms. Among them, there are mutually independent dynamical rules that are fundamental. These basic dynamics rules are called rules, and the motion in the rule space is called rule dynamics [2]. In this paper, a rule rewrites a multiset of the alphabet; we denote a set of alphabets as AL. A multiset, Ms, is defined by a set and a pair of sup functions, <Ms, Sup>, where Sup is a function from the elements of the multiset to a natural number, including zero. For example, SupMs(a) gives the number of occurrences of an in Ms SupMs(a) = two means that Ms contains two a’s, while supMs(a) = 0 means that Ms contains zero a’s. We denote a multiset explicitly as {a, a, b, b, b} = Msi; SupMsi(a) = 2, SupMSi(b) = 3 and SupMSi(c) = 0. A multiset rewriting rule is defined by a pair of multisets, <{l}, {r}>. If Ms, then the intersection of Ms and l is rewritten to r. If {l} ⊆ Ms then {l} is deleted and into {r} is included. For example, the set of rules of rule dynamical expression of LV equations are as follows:
The tri-trophic system in chemical ecology is composed of plants, herbivores, carnivores and HIPV; in the system, plants grow, and if a herbivore eats a plant, the plant generates HIPV, and the herbivore grows; if there is HIPV and herbivores, a carnivore will be attracted and get carnivores to increase population, and the plant stopped generating HIPV. In this scenario, we ignore the increasing population of herbivores and carnivores as the LV equations also ignore the process.
We will denote herbivore as h, carnivores as c and HIPV as d. Based on the scenario, a set of rules of a dynamical expression of the tri-trophic system are as follows.
3. EQUATION OF THE TRI-TROPHIC SYSTEM
In the tri-trophic system in chemical ecology, HIPV is crucial; in the LV equations, carnivores can have herbivores as much as possible, while in the tri-tropihic chemical ecological system, carnivores cannot have herbivores if there is no HIPV. Before herbivores take plants, there is no HIPV, and it is processed in proportion to the number of plants eaten.
The LV equations cannot describe the tri-trophic chemical ecosystem conventionally. LV equations with multi-bodies have been proposed in Dimas Martins [5]. The n species is essentially in a biotrophic system [6–9]. And Sabelis et al. [10] proposed mathematical models of tritrophic system with modified LV equations and game theory in two-species.
Since it is composed of multiple herbivores or carnivores, it can have many bodies interactions between biotrophic layers and cannot have interactions beyond these layers. Therefore, the generalized LV equations cannot essentially describe the chemical ecosystem.
3.1. Transform Dynamical Rule Systems to Differential Equations
We regard the dynamical rule system as a jump Markov process, where every rule is a transition rule; we obtain transition rules of the procedure as r1:p→p,pr2:h,p→h,h,vr3:c,h,v→c,cr4:c→Null, respectively.
We give transition probabilities as
Increments of each rule are (1, 0, 0, 0), (−1, 1, 0, 1), (0, −1, 1, –1) and (0, 0, −1, 0), respectively. Hence, we obtain expectation values of each rule, (5)–(8) gives (9);
Note that this equation is a three bodies LV equation if we ignore v.
3.2. The Behavior of Basic Equations of Chemical Ecosystems
To investigate the behaviors of the model, Equation (13) was embedded in Equation (14) to make it an approximate equations;
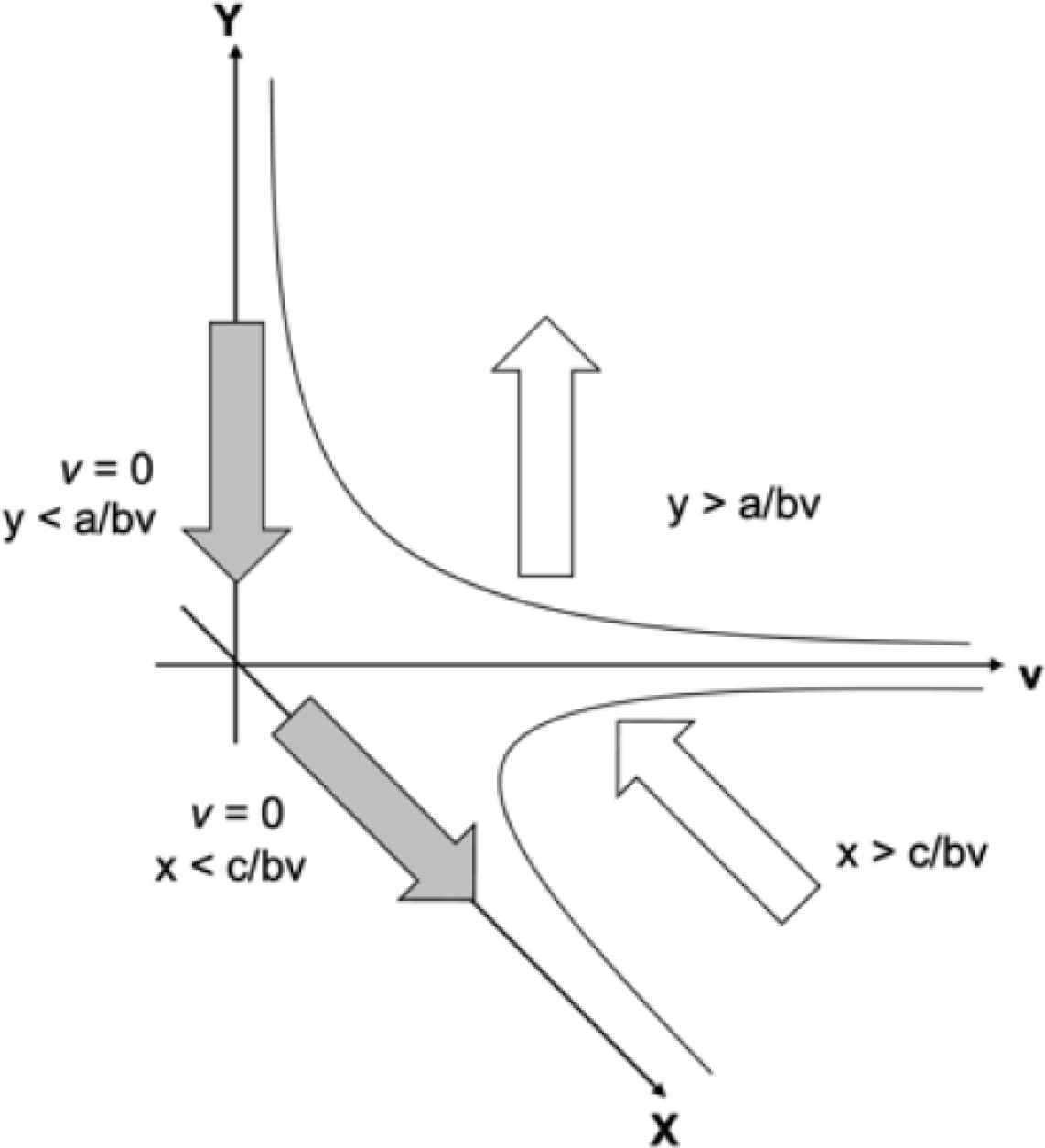
Phase diagram of tri-trophic equations.
4. CONCLUSION
We proposed the equation of three species interactions. We showed that the equilibrium points of this equation are x and y at infinite points including 0. Note that we are considering a positive number including 0, because it is a model of an ecosystem.
In this experiment, the initial values of Herbivores were set to 10 and 100 in increments of 20, while the initial value of carnivores was set to 5. The behaviour of tri-trophic equation was stable at all initial values and did not change significantly (Figure 3).
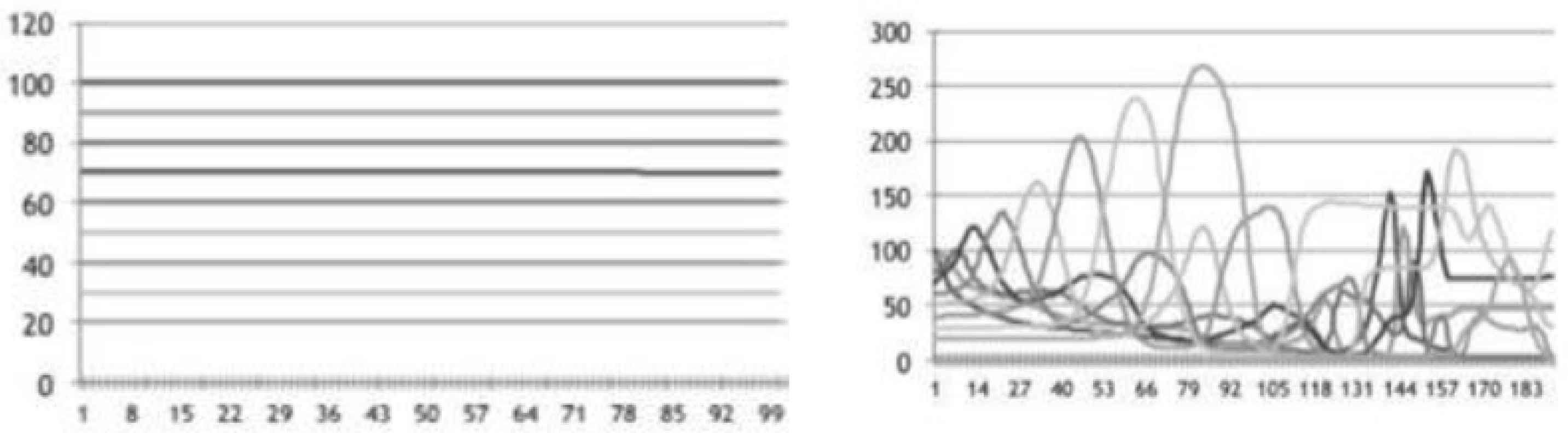
(Left) time developments of 10 species tri-trophic equation, (right) LV equation.
CONFLICTS OF INTEREST
The author declares no conflicts of interest.
AUTHOR INTRODUCTION
Dr. Yasuhiro Suzuki
 He is an Associate Professor of Graduate School of Informatics, Nagoya University Japan. Graduated from Japan Advanced Institute of Science and Technology in 1995, received D. Informatics from Kyoto University in 2001.
He is an Associate Professor of Graduate School of Informatics, Nagoya University Japan. Graduated from Japan Advanced Institute of Science and Technology in 1995, received D. Informatics from Kyoto University in 2001.
REFERENCES
Cite this article
TY - JOUR AU - Yasuhiro Suzuki PY - 2021 DA - 2021/12/27 TI - A Mathematical Model of Tritrophic Systems JO - Journal of Robotics, Networking and Artificial Life SP - 241 EP - 244 VL - 8 IS - 4 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.211108.002 DO - 10.2991/jrnal.k.211108.002 ID - Suzuki2021 ER -
