Distributed Rotating Encirclement Control of Strict-Feedback Multi-Agent Systems using Bearing Measurements
- DOI
- 10.2991/jrnal.k.200512.007How to use a DOI?
- Keywords
- Strict-feedback multi-agent systems; rotating encirclement control; target localization; trajectory planning; trajectory tracking
- Abstract
This paper focuses on the distributed multi-target rotating encirclement formation problem of strict-feedback multi-agent systems using bearing measurements. To this end, an estimator is presented to localize agents’ neighbor targets. Then, based on the trajectory planning method, a reference trajectory is constructed by three estimators, which are utilized to obtain the targets’ geometric center, the reference rotating radius and angular. Finally, an adaptive neural dynamic surface control scheme is proposed to drive all agents to move along their reference trajectories, which satisfy the multi-target rotating encirclement formation conditions. A numerical simulation is provided to verify the correctness and effectiveness of our proposed control scheme.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Recent years have witnessed considerable attention on the rotating encirclement formation problem of multi-agent systems due to its significant potential applications in both military and civilian areas such as surveillance, search-and-rescue, reconnaissance, etc. [1]. Many interesting results have been achieved for the rotating formation or surrounding/encirclement control problem [1–7].
In practice, many physical systems, including manipulators, vessel, unmanned aerial vehicles (UAVs), can be written in the strict-feedback form [8]. Some important researches of the strict-feedback single/multi-agent system have been presented [8–11]. However, there is no research to date on the rotating encirclement control of high-order multi-agent system.
Motivated by the above discussion, for the first time, we consider the multi-target rotating encirclement formation problem of strict-feedback multi-agent systems, and only bearing measurements of targets can be obtained. To this end, we divide the problem into three sub-problems: target localization, trajectory planning and trajectory tracking. Four estimators are designed to construct a reference trajectory for each agent, and an adaptive neural dynamic surface control scheme is presented to drive all agents to move along their desired trajectories.
2. PRELIMINARIES AND PROBLEM STATEMENT
2.1. Graph Theory
Let
2.2. Problem Statement
Consider a multi-target multi-agent system consisting of n agents (Index set
The objective of this note is to design the distributed control scheme using bearing-only measurements of targets and the neighbor position information of agents, such that strict-feedback agents are capable of achieving the multi-target rotating encirclement formation, which is properly formulated by Definition 1 using the polar coordinate transformation
Definition 14.
The multi-agent system is said to achieve the multi-target rotating encirclement formation if
To facilitate the latter control design and analysis, we make some reasonable assumptions.
Assumption 1.
All agents are connected in some undirected communication topologies and each target connected to at least one agent via the directed edge.
Assumption 2.
The radius of the desired rotation formation is bounded, i.e., there exists a positive constant d* satisfying
Assumption 3.
The desired angular velocity ω and angular acceleration
3. CONTROL DESIGN
3.1. Target Localization
With bearing-only measurements, the following estimator is proposed to obtain the neighbor target’s position of agent vi according to Shao and Tian [7].
3.2. Trajectory Planning
We design the following distributed estimators to obtain the estimations
Then, with the polar coordinate transformation, the reference trajectory of agent vi is provided as follows.
3.3. Trajectory Tracking
Define dynamic surface errors as follows.
Then, we present the following adaptive neural dynamic surface control scheme.
4. MAIN RESULTS
With the proposed control scheme in Section 3, we can easily obtain the following reasonable results.
Lemma 1.
Consider the estimator (5) under Assumptions 1–2. Then for any
Proof.
The proof is similar to Theorem 3.1 in Shao and Tian [7].
Then, we define the estimation of the targets’ geometric center as follows.
Apparently,
Lemma 2.
Consider the estimator (6) under Assumptions 1 and 2. For any
Proof.
The proof is similar to Lemma 4 in Zhang et al. [4].
Then, combining Lemma 1 with Lemma 2, we can conclude that the estimation position pi of the i-th agent will asymptotically converge to the actual geometric center
Lemma 3.
Consider the estimator (7) under Assumptions 1 and 2. For any
In other words, the estimation
Proof.
The proof is similar to Lemma 5 in Zhang et al. [4].
Furthermore, with Lemma 1 and 2, it is easy to see that
Lemma 4.
Consider the estimator (8) under Assumptions 1–3. For any
Proof.
The proof is similar to Lemma 6 in Zhang et al. [4].
Thus, from the polar coordinate transformation of (9), we can easily conclude that the reference trajectory
Theorem 1.
Consider the multi-agent system (1) in the strict-feedback form with stationary multi-targets. Suppose that Assumptions 1–3 hold. For any bounded initial condition, if we choose design parameters satisfy ci0 > 0, then all agents will achieve the multi-target rotating encirclement formation with the proposed control scheme in Control Design.
Proof.
The proof is similar to our article at ICAROB2020.
5. NUMERICAL SIMULATION
The strict-feedback multi-agent system, design parameters are chosen as follows and communication topologies are shown in Figure 1.
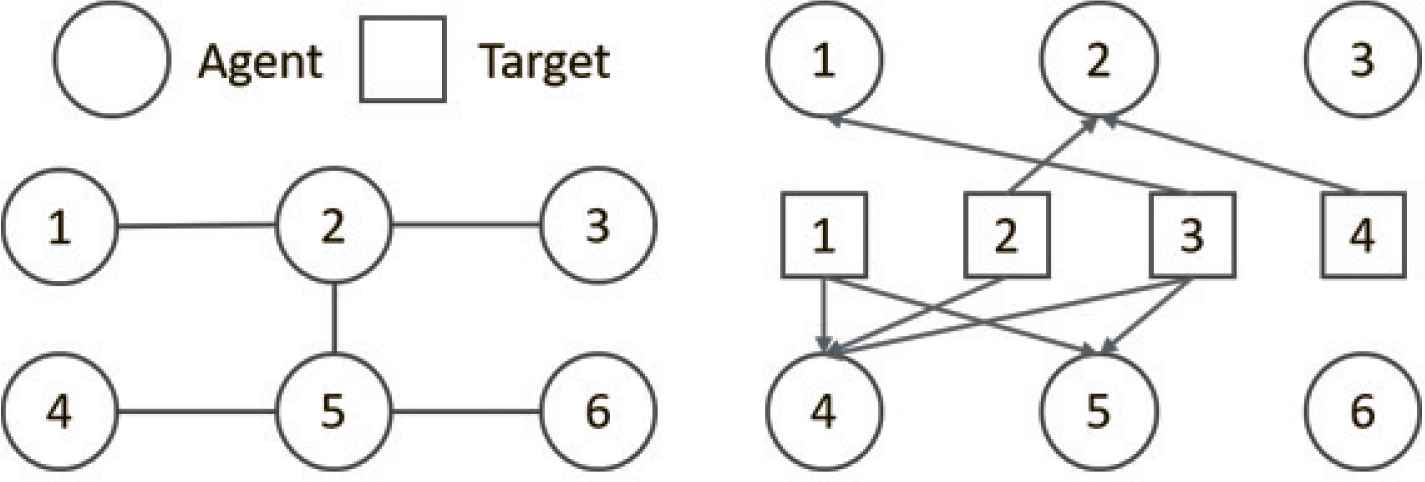
Communication topologies.
Clearly, Assumptions 1–3 are satisfied. Figure 2 shows that all agents can precisely locate their neighbor targets. Figure 3 illustrates that the reference trajectory satisfies conditions in Definition 1. Finally, Figure 4 indicates that the proposed control scheme can force all agents to track their reference trajectories and shows each agent’s trajectory in 3D.
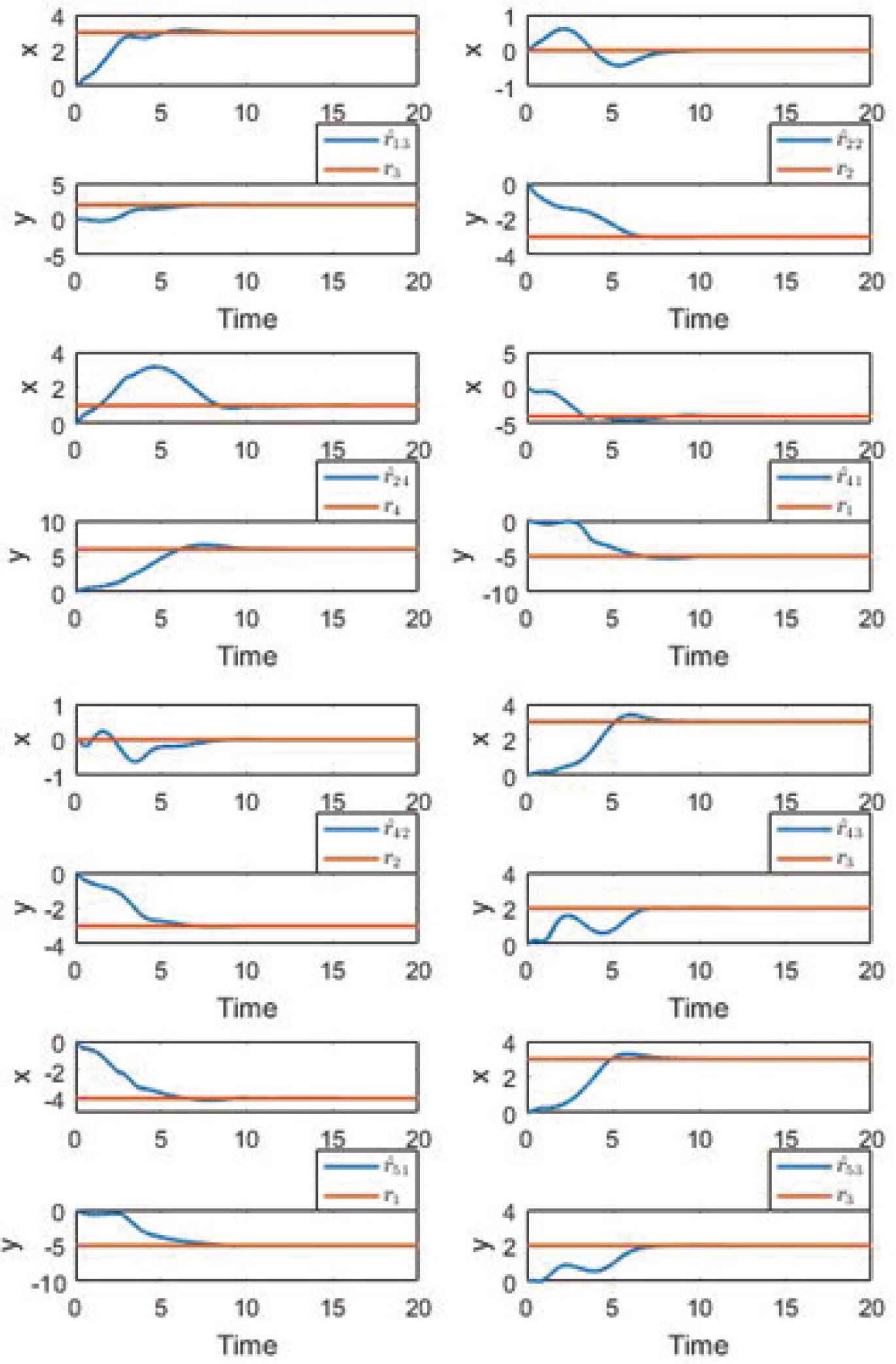
Target localization.
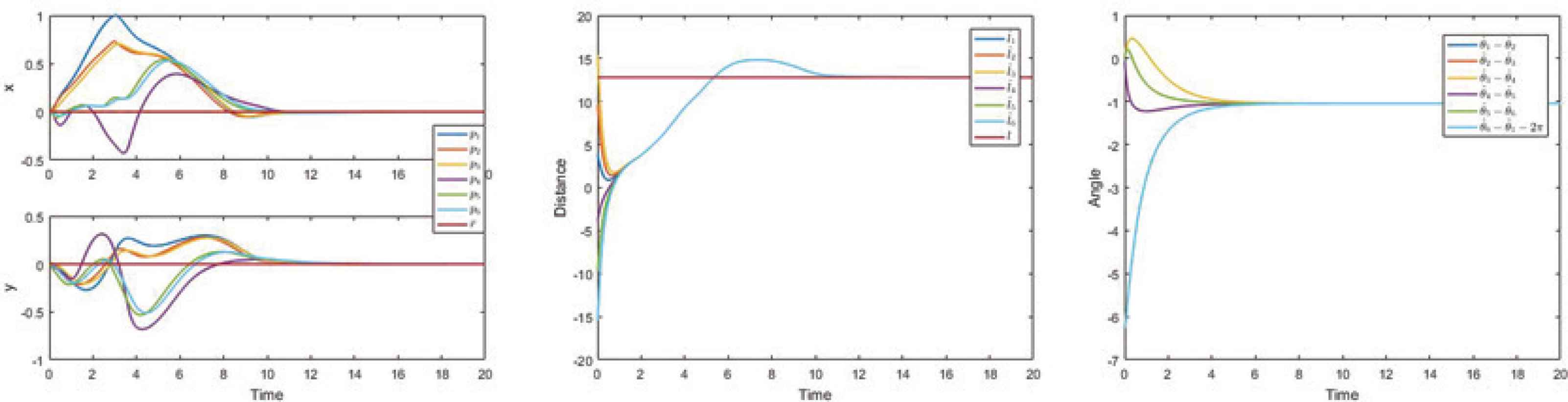
Estimations of the targets’ geometric center, the desired polar radius and polar angle.
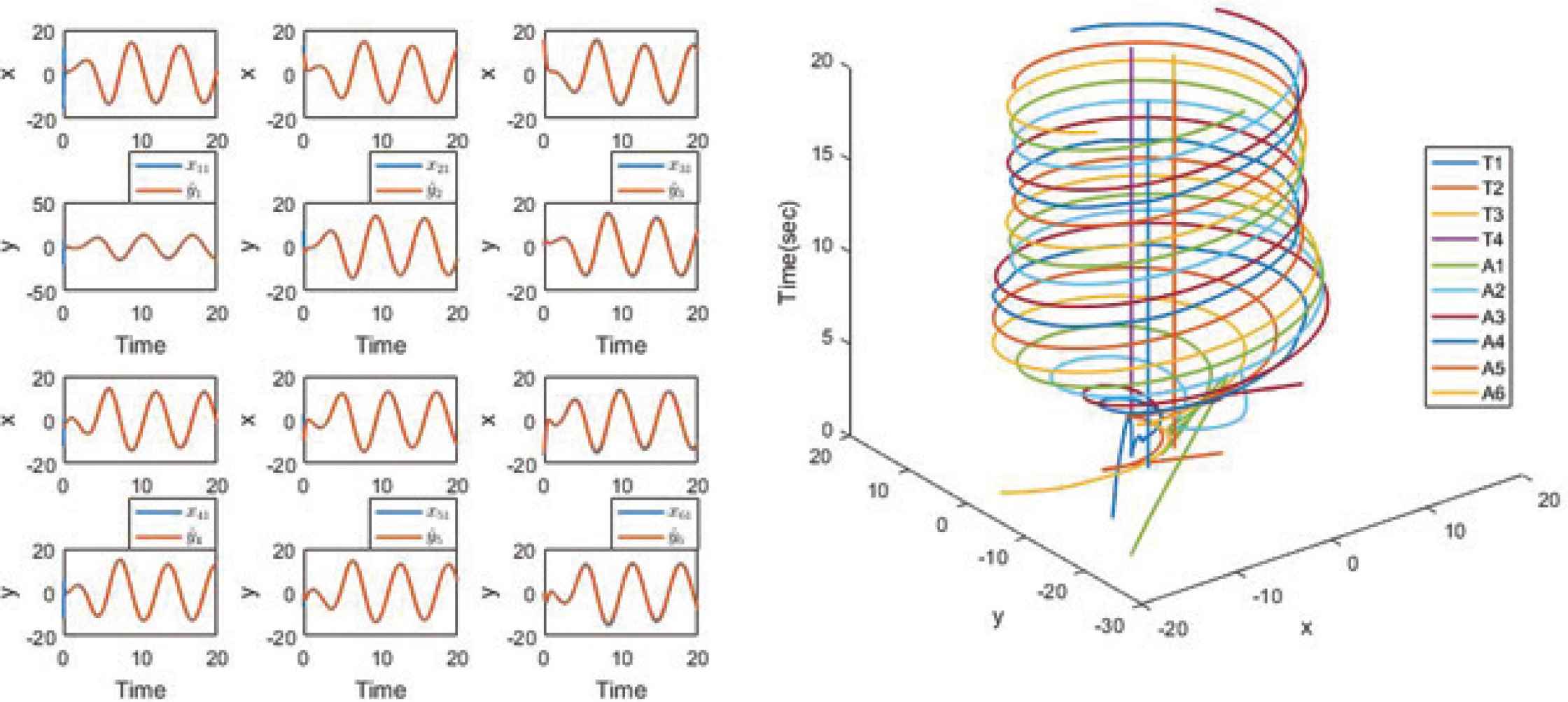
Trajectory tracking and multi-target rotating encirclement formation in 3D.
6. CONCLUSION
The collective multi-target rotating encirclement formation problem of strict-feedback multi-agent systems is investigated by dividing into three sub-problems. Our proposed control scheme can solve this problem well.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENTS
This work was supported by the
AUTHORS INTRODUCTION
Mr. Tengfei Zhang
 He received the B.S. degree in information and computational science from Beihang University, Beijing, China, in 2016. He is currently pursuing the PhD degree with the Seventh Research Division and the Center for Information and Control, School of Automation Science and Electrical Engineering, Beihang University. His current research interests include cooperative control of multiagent systems.
He received the B.S. degree in information and computational science from Beihang University, Beijing, China, in 2016. He is currently pursuing the PhD degree with the Seventh Research Division and the Center for Information and Control, School of Automation Science and Electrical Engineering, Beihang University. His current research interests include cooperative control of multiagent systems.
Prof. Yingmin Jia
 He received the B.S. degree in control theory from Shandong University, China, in 1982, and the M.S. and PhD degrees both in control theory and applications from Beihang University, China, in 1990 and 1993, respectively. Then, he joined the Seventh Research Division at Beihang University where he is currently Professor of automatic control. From February 1995 until February 1996 he was a Visiting Professor with the Institute of Robotics and Mechatronics of the German Aerospace Center (DLR), Oberpfaffenhofen, Germany. He held an Alexander von Humboldt (AvH) research fellowship with the Institute of Control Engineering at the Technical University Hamburg-Harburg, Hamburg, Germany, from December 1996 until March 1998, and a JSPS research fellowship with the Department of Electrical and Electronic Systems at the Osaka Prefecture University, Osaka, Japan, from March 2000 until March 2002. He was a Visiting Professor with the Department of Statistics at the University of California Berkeley from December 2006 until March 2007. Dr. Jia was the recipient of the National Science Fund for Distinguished Young Scholars in 1996, and was appointed as Chang Jiang Scholar of the Ministry of Education of China in 2004. He has been Chief Scientist of the National Basic Research Program of China (973 Program) since 2011, and in particular he won the Second Prize of National Technology Invention Award in 2015. His current research interests include robust control, adaptive control and intelligent control, and their applications in robots systems and distributed parameter systems.
He received the B.S. degree in control theory from Shandong University, China, in 1982, and the M.S. and PhD degrees both in control theory and applications from Beihang University, China, in 1990 and 1993, respectively. Then, he joined the Seventh Research Division at Beihang University where he is currently Professor of automatic control. From February 1995 until February 1996 he was a Visiting Professor with the Institute of Robotics and Mechatronics of the German Aerospace Center (DLR), Oberpfaffenhofen, Germany. He held an Alexander von Humboldt (AvH) research fellowship with the Institute of Control Engineering at the Technical University Hamburg-Harburg, Hamburg, Germany, from December 1996 until March 1998, and a JSPS research fellowship with the Department of Electrical and Electronic Systems at the Osaka Prefecture University, Osaka, Japan, from March 2000 until March 2002. He was a Visiting Professor with the Department of Statistics at the University of California Berkeley from December 2006 until March 2007. Dr. Jia was the recipient of the National Science Fund for Distinguished Young Scholars in 1996, and was appointed as Chang Jiang Scholar of the Ministry of Education of China in 2004. He has been Chief Scientist of the National Basic Research Program of China (973 Program) since 2011, and in particular he won the Second Prize of National Technology Invention Award in 2015. His current research interests include robust control, adaptive control and intelligent control, and their applications in robots systems and distributed parameter systems.
REFERENCES
Cite this article
TY - JOUR AU - Tengfei Zhang AU - Yingmin Jia PY - 2020 DA - 2020/05/20 TI - Distributed Rotating Encirclement Control of Strict-Feedback Multi-Agent Systems using Bearing Measurements JO - Journal of Robotics, Networking and Artificial Life SP - 30 EP - 34 VL - 7 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.200512.007 DO - 10.2991/jrnal.k.200512.007 ID - Zhang2020 ER -
