An Error Correction Mechanism for Reliable Chemical Communication Systems
- DOI
- 10.2991/jrnal.k.200512.011How to use a DOI?
- Keywords
- Bio-inspired communication; chemical reaction network; chemical sensory system; error correction; kinetic proofreading
- Abstract
Chemical communication systems, such as bio-inspired chemical sensory systems or biological cells, sense the environment by detecting target ligand molecules, which convey environmental information. However, non-target ligands, similar to the target ones, are ubiquitous in the environment and can hamper accurate information transmission. In this work, we investigate an error correction mechanism for reliable chemical communications and find an intuitive understanding of how the mechanism can amplify the small difference between the target and non-target ligands. We also demonstrate that the mechanism can balance accuracy and output intensity. Our approach may provide a method to design reliable chemical communication systems.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Chemical communication systems, such as bio-inspired chemical sensory systems or biological cells, sense the environment by detecting target ligand molecules, which convey environmental information [1]. The chemical communication system detects the target ligands using receptor molecules, which act as sensors for environmental information. However, non-target ligands, similar to the target ones, are ubiquitous in the environment. Due to the structural similarity, the non-target ligands have affinities to the receptors and can attach to the receptor molecules. This non-specific and undesired interaction may send an erroneous signal into the system and hamper accurate information transmission. Even under the effect of non-target ligands, biological cells such as immune T cells or chemical reaction systems for the translation and transcription of genetic information have high fidelity to the target ligands [2–6].
The series of experimental observations suggest that biological systems have some error correction mechanisms to detect the target ligands for reliable chemical communication. To reveal the underlying mechanism of the biological error correction systems for chemical communications, the zero-order proofreading model [7] was recently proposed as an extended model of the kinetic proofreading model, which is the pioneering works by Hopfield and Ninio for a biological error correction mechanism [8,9].
In this paper, we first model chemical sensing. Then we introduce the zero-order proofreading model [7] and investigate the intuitive understanding of how the model can precisely discriminate the target ligand from the similar non-target one based on their affinity parameters. We further investigate the target detection performance of the zero-order proofreading model under the condition that the target and non-target ligands exist in the environment simultaneously.
2. ZERO-ORDER PROOFREADING MECHANISM FOR ULTRA-SPECIFICITY
2.1. Modeling of Chemical Sensing
We start with considering the simplest situation that only a single type of ligand molecule exists in the environment (Figure 1). In this situation, a chemical communication system or a cell distinguishes whether the ligand molecule is the target ligand or non-target one by using receptor molecules, which work as chemical sensors for the environmental signal. The receptor R can detect the ligand L, and the ligand–receptor binding and unbinding reactions are described as follows:
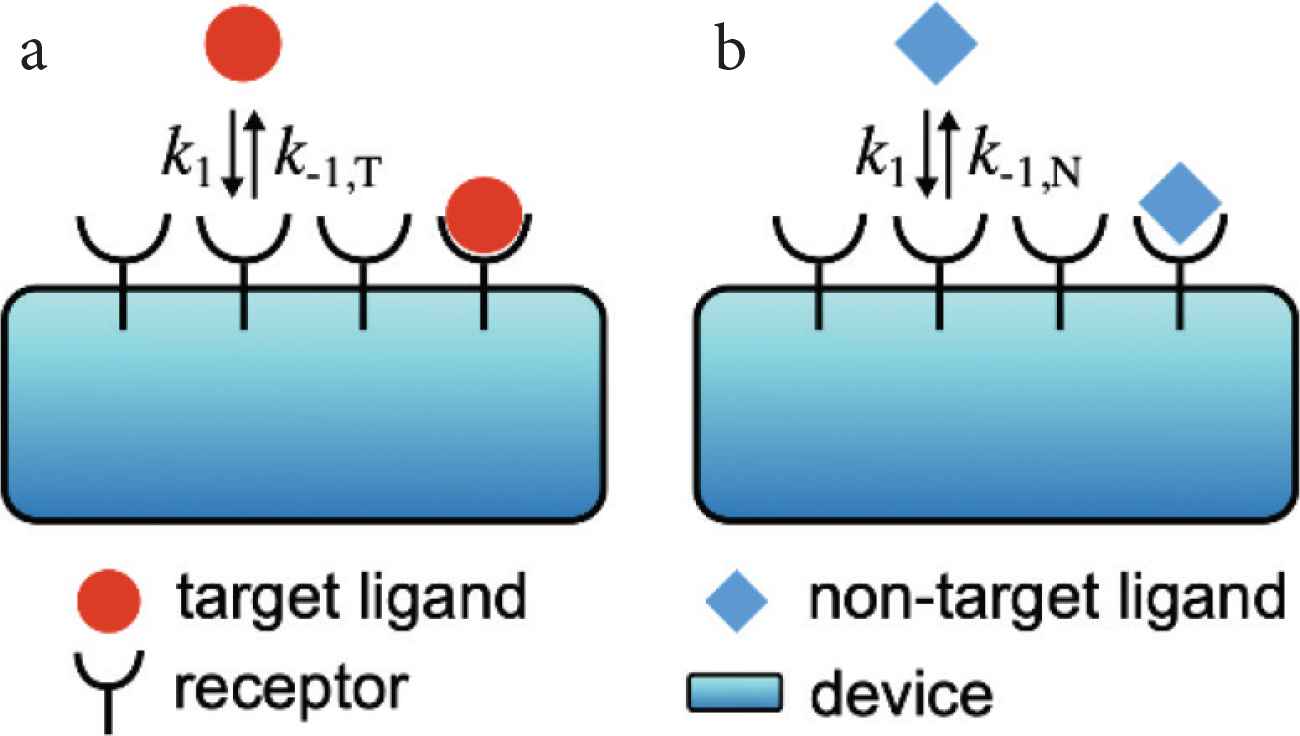
Schematics of a chemical communication system when (a) the target ligand molecule or (b) non-target one exists in the environment. The reaction constants of the binding and unbinding reactions are respectively k1(s−1M−1) and k−1*(s−1) where * is T and N for the target ligand and non-target one, respectively. We assume that k−1,T(s−1) < k−1,N(s−1) because the non-target ligand is more likely to dissociate from the receptor.
We assume that the target and non-target ligands have similar sizes and structures. Then, we can assume that the difference between the target and non-target ligands is only the unbinding rate k−1 (Figure 1). If we denote the unbinding rates of the target ligand k−1,T(s−1) (Figure 1a) and that of the non-target one k−1,N(s−1) (Figure 1b), the unbinding rates satisfy k−1,T(s−1) < k−1,N(s−1) because the non-target ligand is more likely to dissociate from the receptor.
2.2. Zero-order Proofreading Model
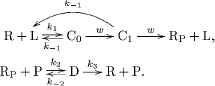
If the target and non-target ligands are similar molecules, the difference in the unbinding rates among k−1,T(s−1) and k−1,N(s−1) is small. For reliable chemical communications, the system must amplify the small difference of the unbinding rate k−1. To this end, the following phosphorylation and dephosphorylation cycle was proposed in Kajita et al. [7] as an intracellular chemical reaction network that can amplify the small difference in k−1 (see also Figure 2):
 (2)
(2)
After the formation of the ligand–receptor complex C0, the receptor can be converted into the intermediate state of the complex denoted by C1 with rate w(s−1) via an irreversible reaction. The product RP can be generated from C1 with rate w. However, some of C1 can be converted back to R + L due to the ligand dissociation from the receptor with rate k−1. Note that we assume that the two unbinding reactions, C0 → R + L and C1 → R + L, have the same rate k−1 [8–10]. This assumption is valid if the chemical modification of the receptor, which is carried out by the reaction C0 → C1, only affects the intracellular part of the receptor and does not affect the unbinding rate k−1. We also note that the unbinding reaction C1 → R + L is an irreversible reaction for an error correction function, which is called kinetic proofreading [8–10]. The product RP is covalently modified and activated receptor R, and RP can be deactivated by an enzyme P. D denotes the complex of RP and P. The reaction constants of the binding and unbinding reactions are k2(s−1M−1) and k−2(s−1), respectively. The receptor R is generated from D with rate k3(s−1).

Schematic diagram of the zero-order proofreading model [Equation (2)] in a chemical communication system. The receptors detect the ligands in the environment, then transmit the signal into the inside of the system using the chemical reactions. The system distinguishes whether the ligand is the target ligand or not by converting the unbinding rate k−1 into the amount of the product molecules [RP] through the zero-order proofreading model.
2.3. Model Reduction Based on Michaelis–Menten Approximation
By assuming that each reaction follows the law of mass action, the dynamics of the zero-order proofreading model [Equation (2)] can be described by Ordinary Differential Equations (ODEs). To obtain an intuitive understanding of how the zero-order proofreading model amplifies the small difference among the target and non-target ligands, we perform a model reduction based on Michaelis–Menten approximation [11].
If the total concentration of receptor [R]total:= [R] + [RP] + [C0] + [C1] + [D] is much larger than those of ligand and enzyme, [L]total:= [L] + [C0] + [C1] and [P]total:= [P] + [D], [RP]total ≈ [R]total ≈ [R] + [RP] holds, where [X] denotes the concentration of molecule X, whose unit is [M]. At the quasi steady state, that is, d[C1]/dt = d[C0]/dt = d[P]/dt = 0, the dynamics of [RP] can be described by the following ODE:
The production speed of [RP] can be decomposed into the positive and negative fluxes, which are denoted as J1 and J2, respectively. The definitions are
Thus, the net flux is given by J:= d[RP]/dt = J1 − J2. These Equations (4) and (5) are called Michaelis–Menten equations [11].
The parameters Km,1 and K2 are the effective Michaelis–Menten constants of the positive and negative fluxes, respectively. Note that Km,1 and K2 respectively control the ligand and enzyme saturation levels. At the unsaturated condition, when Km,1 >> [RP]total and K2 >> [RP]total, Equations (4) and (5) become
These fluxes are approximately the first-order reactions with respect to [RP], which are demonstrated in Figure 3a. On the other hand, at the saturated condition, when Km,1 ≪ [RP]total and K2 ≪ [RP]total, Equations (4) and (5) become
These approximated equations do not depend on [RP], thus these are called zero-order reactions with respect to [RP], which are also demonstrated in Figure 3b.

Fluxes of the activation and deactivation reaction cycle of the zero-order proofreading model [Equation (2)] when the system is in an unsaturated condition (a) and a saturated condition (b). The positive flux J1 [Equation (4)] with the target ligand (red lines), with the non-target ligand (red dashed lines), and the negative flux J2 [Equation (5)] (blue lines) are plotted as functions of [RP]. The steady states with the target ligand are plotted as red circles, and the steady states with the non-target one are plotted as blue rhombuses in the figures. Here, K denotes the effective Michaelis–Menten constants, which controls the unsaturation level of J1 and J2, respectively, where K = Km,1 = K2. The displayed values of K are set for the target ligand, and k−1 and k2 are obtained from the values of K. The other parameters are k−1 = 1 for the target ligand, k−1 = 2 for the non-target one, w = 1, k−2 = 10, k3 = 1, [R]total = 100, [L]total = 3.5, and [P]total = 1.
2.4. An Intuitive Understanding of the Zero-order Proofreading Mechanism
Next, we clarify the mechanism of how the saturation level affects the response of the zero-order proofreading model to the unbinding rate k−1. At the steady state, J1 = J2 holds. By solving J1 = J2 for [RP], we can obtain the steady state concentration of [RP], denoted as [RP]*. Because J1 depends on the unbinding rate k−1, [RP]* also depends on k−1. This means that [RP]* changes depending on whether the ligand is the target or not. To investigate how the saturation level changes the difference in the steady-state concentrations [RP]* for the target and non-target ligands, we analyze the dependence of the fluxes, Equations (4) and (5), on the unbinding rate k−1. When the system is in unsaturated condition (Figure 3a), the small change in k−1 slightly affects J1. Because of the small effect, the steady-state concentrations [RP]* for the target and non-target ligands do not differ largely. On the other hand, when the system is saturated (Figure 3b), even though the small difference in k−1 slightly changes the positive flux, J1 ≈ V1 = wα [L]total/(1 + α) = w2/(k−1 + 2w), due to the zero-order reactions, the steady state concentration [RP]* largely moves. This is an intuitive understanding of how the zero-order proofreading model [Equation (2)] [7] can amplify the small difference of the unbinding rate k−1 between the target and non-target ligands by changing the saturation level.
Note that the highly nonlinear response due to the cycle reaction composed of the two zero-order reactions is called zero-order ultra-sensitivity [11,12]. Although the original model proposed by Goldbeter and Koshland [12] has the ultra-sensitivity to concentration variables ([L]total and [P]total in the zero-order proofreading model), the model cannot amplify the unbinding rate k−1. Our representation in Figure 3 clarifies how the zero-order proofreading model obtains the ultra-specificity to the target ligand by the nonlinearity to the unbinding rate k−1 based on the mechanism of the zero-order reaction.
3. THE CASE OF TWO LIGANDS IN THE ENVIRONMENT
Let us consider a more realistic condition for chemical communication systems, that is, the system is surrounded by more than one type of ligand. As the simplest case, we consider that there are two types of ligands, the target and non-target ligands, exist in the environment simultaneously (Figure 4). In this situation, we investigate how the zero-order proofreading mechanism contributes to the reliable detection of the target ligand.

Schematics of a chemical communication system when the target and non-target ligands exist in the environment simultaneously.
When there are two ligands, the zero-order proofreading model can be extended as follows (see also Figure 5):
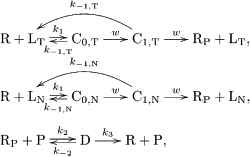 (10)
(10)
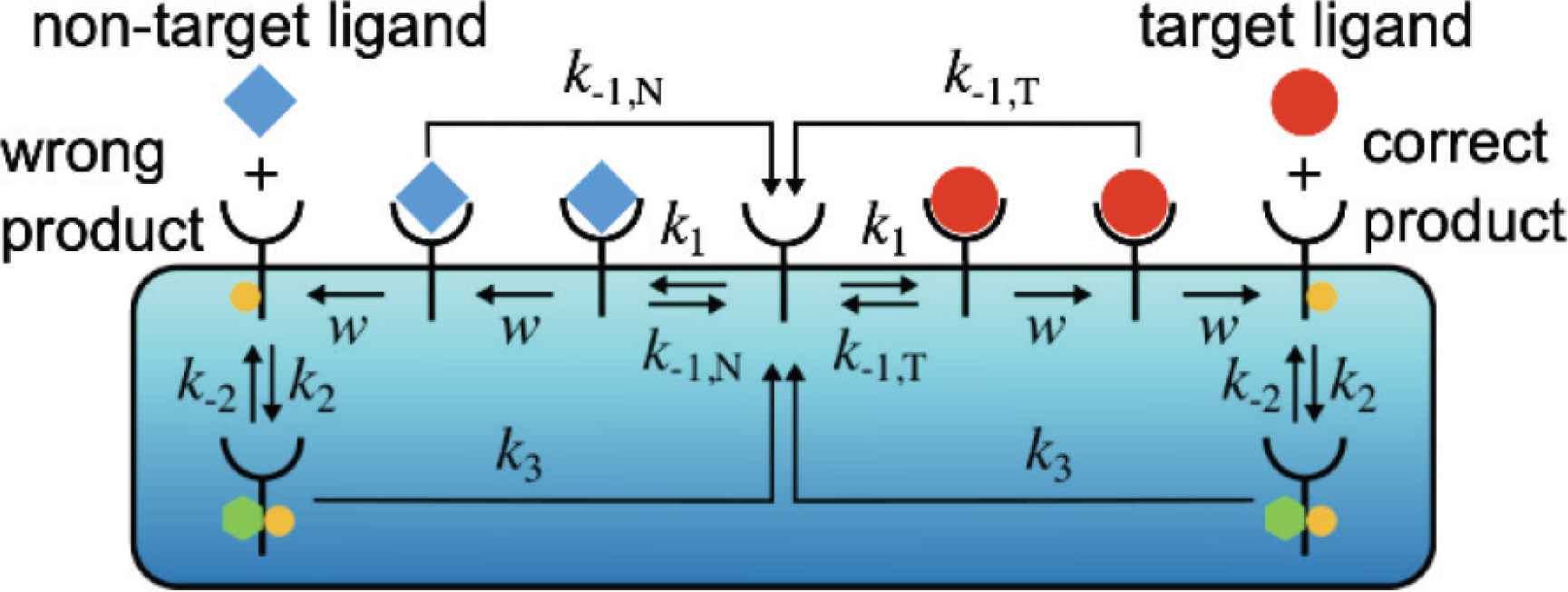
Schematics of the zero-order proofreading model when the target and non-target ligands exist simultaneously in the environment.
3.1. Model Reduction based on Michaelis–Menten Approximation
As we did the model reduction of the zero-order proofreading for the single type of ligand, we apply the Michaelis–Menten approximation to the zero-order proofreading model for two types of ligands [Equation (10)].
Assume that the dynamics of Equation (10) follows the law of mass action, then the dynamics can be described by ODEs. If we also assume that the total concentration of receptor [R]total:= [R] + [RP] + ∑i,*[Ci,*] + [D] is much larger than those of the target ligand, [LT]total:= [LT] + ∑i,*[Ci,T], non-target ligand, [LT]total:= [LT] + ∑i,*[Ci,T], [LN]total:= [LN] + ∑i,*[Ci,N], and enzyme, [P]total:= [P] + [D], then [R]total ≈ [R] + [RP] holds. At the quasi-steady-state, that is, d[C1,*]/dt = d[C0,*]/dt = d[P]/dt = 0 for * ∈{T, N}, the dynamics of RP can be described by the following ODE with respect to [RP]:
3.2. The Reliability of the Zero-order Proofreading Model
To evaluate the performance of the target ligand detection, we introduce the following quantities. First, we introduce the True Positive (TP) and False Positive (FP) by using the partial flux to produce the product molecule RP by the target ligand and that by the non-target one, which are defined respectively by
By using TP and FP, we introduce the error η to evaluate the reliability of the target detection, which is defined as
For a reliable chemical communication, the balance between the accuracy and the intensity of output is necessary. For example, even if the error is low, but the output intensity from the sensory system is quite small, there is a risk that the output signal may disappear before the subsequent reactions are induced inside of the communication system. To evaluate the intensity of output, we introduce the output intensity O, which is defined by
To analyze the effect of the absence of non-target ligands, we introduce the fraction of the target ligand [13],

The error η (red dots) and the output intensity O (blue squares) are plotted as functions of the target ligand fraction r (a and b) and the unbinding rate ratio Δ (c and d) for different values of K, where K = Km,T = K2. The parameters are k−1,T = 1, Δ = 1/10 (a and b), r = 1/2 (c and d), w = 1, k−2 = 10, k3 = 1, [R]total = 100, and [L]total = 5. Note that k1 and k2 are obtained from the value of K, [L*]total for * ∈{T,N} is obtained from r (a and b), and k−1,N is obtained from Δ (c and d).
To investigate the effect of similarity between the target and non-target ligands, we introduce the unbinding constant ratio
As same as in Figure 6a and b, the error of saturated condition (Figure 6c) is always slightly higher than those of unsaturated condition (Figure 6d). However, these two cases have the same tendency that the error decreases when the difference between the target and non-target ligands Δ becomes large. In contrast, the response of the output intensity O to Δ again shows a qualitatively different dependency on the unsaturation level K. When the system is saturated (Figure 6c), the response of O to Δ shows an all-or-none response. In addition, in this saturated condition, the system can generate large output O even when Δ is small, which means that the system can generate a large output without the help of the non-target ligand. With an increase in the unsaturation level (Figure 6d), the response becomes more gradual, and the system cannot generate large output O in the range where the error η is small (for e.g. Δ ∈ [0.0, 0.3]). As the results, at the saturated condition (Figure 6c), the system can balance the high accuracy and large output O around Δ ∈ [0.1, 0.2].
We also investigate the dependencies of the error η and output intensity O on both the target ligand fraction r and the unbinding constant ratio Δ for various saturation levels K (Figure 7), and confirm that the qualitatively same results in Figure 6 hold for the various values of K. Together with the results in Figures 6 and 7, the zero-order proofreading mechanism with saturating condition can balance the high accuracy and large output O at the slight cost of the error η.

The error η (a and c) and the output intensity O (b and d) are plotted as functions of the target ligand fraction r and the unsaturation level K (a and b), and the unbinding rate ratio Δ and the unsaturation level K (c and d), where K = Km,T = K2. The parameters are k−1,T = 1, w = 1, k−2 = 10, k3 = 1, [R]total = 100, and [L]total = 5. The others are Δ = 1/10 for (a and b), and r = 1/2 for (c and d). Note that k1, k2, [L*]total for * ∈{T,N} (a and b), and k−1,N (c and d) are obtained in the same manner as in Figure 6.
4. SUMMARY AND DISCUSSION
In this work, we analyzed the zero-order proofreading model [7] and obtain an intuitive understanding of how the mechanism amplifies the unbinding rate from the viewpoint of the balance of the positive and negative fluxes in a saturated condition. We further demonstrated that the zero-order proofreading model is valid for the case that there are the target and non-target ligands in the environment simultaneously, by revealing that the model with saturated conditions can balance both the accuracy and output intensity. The zero-order proofreading mechanism may not only give an insight into how biological cells perform reliable chemical communications in the complex mixtures of ligands, but also provide a method to design bio-inspired reliable chemical communication systems.
CONFLICTS OF INTEREST
The author declares no conflicts of interest.
ACKNOWLEDGMENTS
I would like to thank Tetsuya J. Kobayashi and Kazuyuki Aihara for fruitful discussion. This work was supported by
AUTHOR INTRODUCTION
Dr. Masashi K. Kajita
 He is an Assistant Professor in the Department of Applied Chemistry and Biotechnology at University of Fukui. He received his PhD degree from the University of Tokyo in 2017. From October 2017 to February 2020, he had worked in the University of Tokyo as a Research Associate. Since March 2020, he has been in University of Fukui. His current research interests are biochemical information processing, and data-driven modeling of biological systems.
He is an Assistant Professor in the Department of Applied Chemistry and Biotechnology at University of Fukui. He received his PhD degree from the University of Tokyo in 2017. From October 2017 to February 2020, he had worked in the University of Tokyo as a Research Associate. Since March 2020, he has been in University of Fukui. His current research interests are biochemical information processing, and data-driven modeling of biological systems.
REFERENCES
Cite this article
TY - JOUR AU - Masashi K. Kajita PY - 2020 DA - 2020/05/20 TI - An Error Correction Mechanism for Reliable Chemical Communication Systems JO - Journal of Robotics, Networking and Artificial Life SP - 52 EP - 57 VL - 7 IS - 1 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.200512.011 DO - 10.2991/jrnal.k.200512.011 ID - Kajita2020 ER -
