1. INTRODUCTION

RoboCup is an international project that promotes innovation in Artificial Intelligence (AI), robotics, and related domains. It represents an attempt to develop AI and autonomous robotics research by providing a fundamental problem that can be solved by integrating a wide range of technologies. In particular, the middle-size league soccer competition is a RoboCup event providing a dynamical environment in which many robots cooperate with humans within the same space.

Various developments have been made in the RoboCup middle-size league soccer robot [1,2]. These robots generally have a mechanism similar to that of an omnidirectional movement mechanism using three-omni wheels [3] or that using four-omni wheels [4] and so on, and in recent years, this mechanism is involved in controlling the rotation of a ball. The ball holding mechanism is used.

In the past, several teams have equipped their robots such as arm type [5,6], bar type [7,8] and single-wheel type [9] with ball dribbling mechanisms for controlling the rotation of the ball. To be useful in soccer play, the dribbling performance of such mechanisms must be skillful. However, they cannot grasp a ball and control. Recently, dribbling devices use rollers to grasp the upper half of the ball to enable them to maintain a pull on it while driving in reverse. Friction is generated between the ball and rollers by a spring mounted on a supporting lever. To maintain dribbling, it is essential that the roller and ball rotate with approximately the same speed and that the ball moves in the same direction as the robot. Many robots, such as that deployed by the Turtles team [10], rely on ball handling force and use a roller arrangement in which there is slip between the roller and ball. To determine their roller arrangement, the Turtles rely on heuristic measures and experimental results. Although slip causes loss of speed in a moving sphere, the resulting friction can improve the ball holding power and rotational stability. Accordingly, slip is an important factor.

The authors conducted an investigation of the ball dribbling mechanisms employed by the teams at the 2017 middle-size league soccer competition in Nagoya, Japan. Table 1 lists our survey results, including team name and roller type, shape, and arrangement angle. The four shapes [◻⚪△◇] in the “Symbol” column indicate the roller angles used by the respective teams. Figure 1 shows the rotational axis, ball velocity, and roller velocity in reverse motion of a dual-roller arrangement. The RV-Infinity [11] roller arrangement in Table 1 involves no slip (see Figure 1a) because the roller velocity corresponds to the ball velocity; i.e., the rollers’ rotational axes are aligned on a plane that includes the origin of the ball’s sphere [12,13]. In another approach, CAMBADA [14] avoids slippage through the use of unconstrained rollers (omni-rollers).

Figure 1

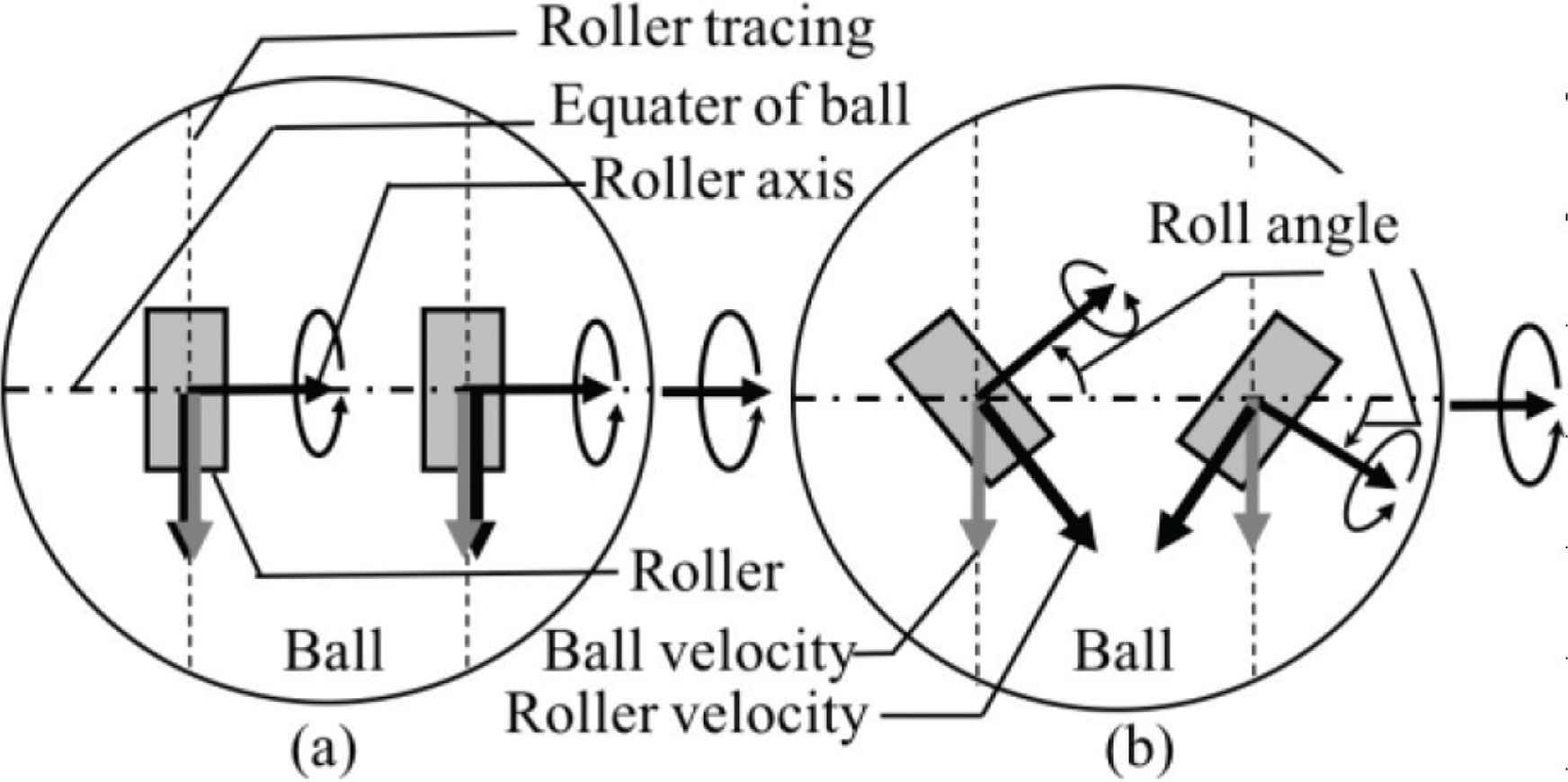
The ball reverse motion by two-rollers arrangement in the ball-dribbling mechanism. Case of (a) is zero-roller angle and case of (b) is non-zero-roller angle.

Other teams, namely the Turtles [10], Falcons, Musashi150 [15], NuBot [16], and Water, have adopted roller arrangements that allow for slip to occur (see Figure 1b) through a differential between roller and ball velocity. Based on analysis of sphere rotational motion in which slip is allowed, we developed a sphere kinematics model in which dual-constraint rollers allow for slipping [17].

In this study, we validated the model introduced in Kimura et al. [17] and evaluated the roller arrangements used by the competition teams from the standpoint of sphere speed, efficiency, and sphere slip speed (ball-holding power).

The remainder of this paper is organized as follows. In Section 2, we introduce a sphere kinematics model that allows for slipping. In Section 3, we validated the model introduced in Kimura et al. [17] and theoretical formula of sphere slip velocity vector. In Section 4, we considered the distribution of slip velocity vector and the roller arrangement of a ball dribbling mechanism based on the results of a robotic experiment. Finally, in Section 5, we present a summary and discuss future research.

2. THE SLIP VELOCITY VECTOR OF THE SPHERE

We quantify the slip between the sphere and roller.

As shown in Figure 2a, the center O of a sphere with radius r is fixed as the origin of the coordinate system ∑ − xyz. The i-th constraint roller is in point contact with the sphere at a position vector P_i and is arranged such that the center of mass of the roller P_C, P_i and O are on the same line. ω denotes the angular velocity vector of the sphere. η_i denotes the unit vector along the rotational axis of constraint roller. ν_i the denotes peripheral speed of the constraint roller. α_i (−90° ≤ α_i ≤ 90°) denotes roller arrangement angle between η_i and span{P₁, P₂} which has unit normal vector e. The great circle C_G passes thorough P₁ and P₂ are on the sphere. Normal orthogonal base {X_i, e} exist on the tangent plane span{X_i, e} at the P_i (see Figure 2b and 2c). 𝒱iS and 𝒱iR are sphere’s rotational speed and roller’s rotational speed at P_i, respectively. The slip velocity of sphere ζ_i can be represented as difference between 𝒱iS and 𝒱iR. ζ_i can be represented as S_iX_i + T_ie (linear combination of X_i and e) and the coefficients S_i and T_i can be represented as Equations (1)–(3).

Figure 2

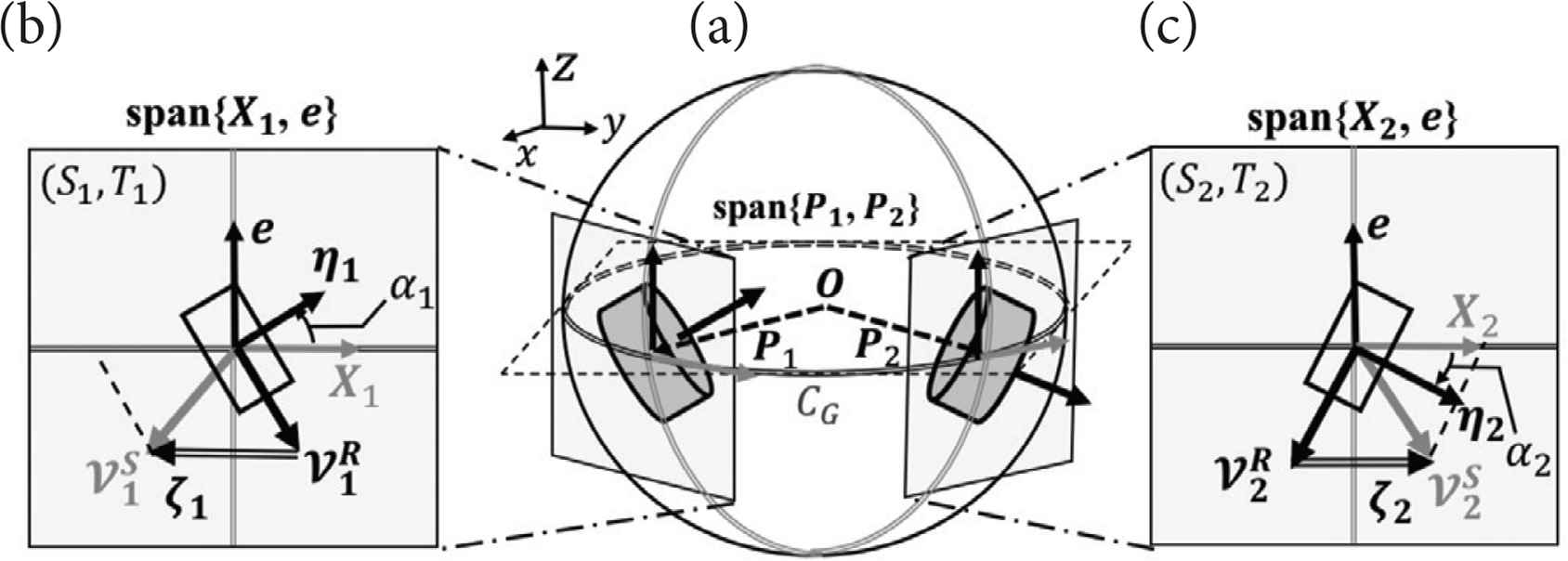
The existence of sphere slip velocity vector. (a) Isometric view. (b) Left side roller on span{X₁, e}. (c) Right side roller on span{X₂, e}.

3. VERIFICATION OF THEORETICAL FORMULA

In this chapter, we verified theoretical formulas including sphere kinematic (Section 3.1) and sphere slip velocity vector (Section 3.2) in reverse motion.

As shown in Figure 3, the conditions are given as follows: θ_1,1 = 215°, θ_1,2 = 325°, θ_1,2, θ_2,2 = 60°, r = 0.1 (m), α₁ = α, α₂ = −α (symmetry roller arrangement). Five experiments were conducted, each at the same four different degrees angles (α = 0°, 10°, 20°, 30°).

Figure 3

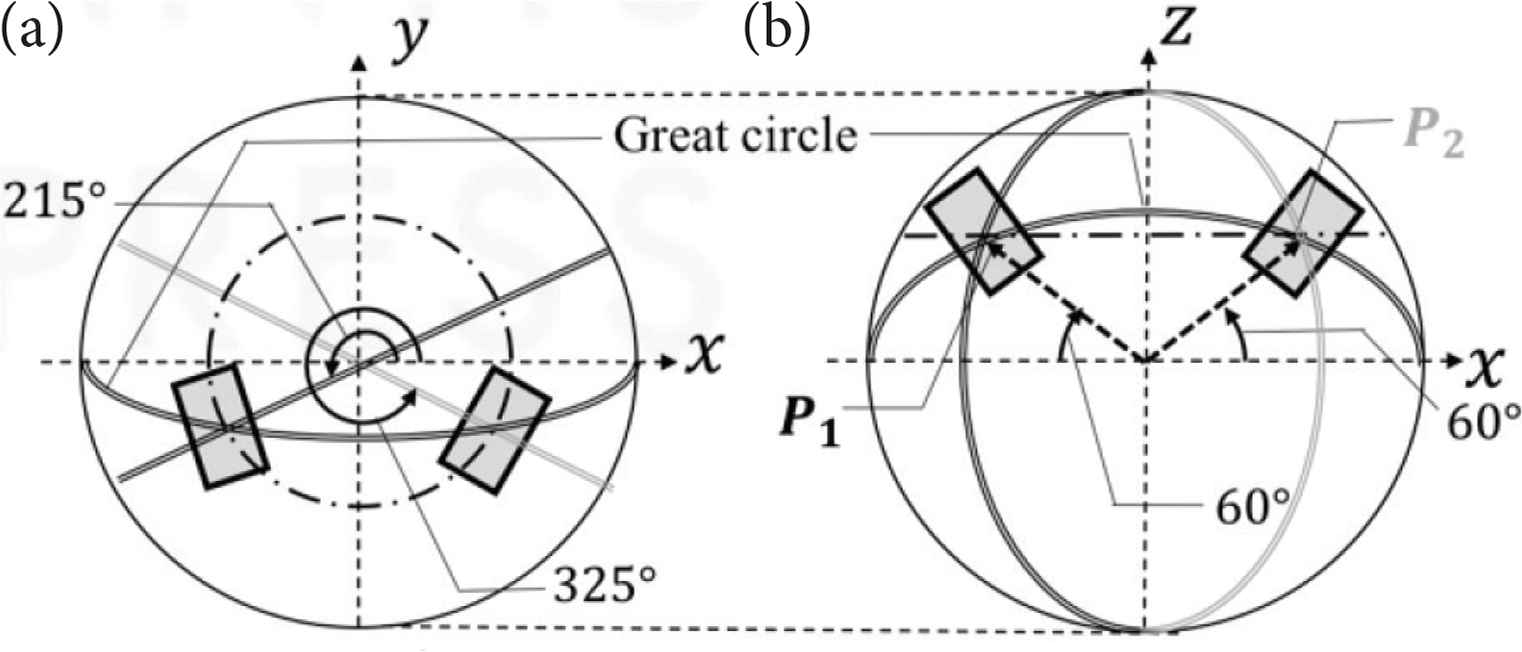
The location of contacted rollers on sphere for experiment. (a) Top view. (b) Back view.

3.1. Verification of Kinematics

As shown in Table 2, ||V||, φ and ρ are values calculated from v₁, v₂ = −0.91 (m/s) by Equations (11) and (14) refer to Kimura et al. [17]. ν1m, ν2m are theoretical values (controlled values which have target values v₁, v₂ = −0.91 (m/s)). ||V||_m, φ_m and ρ_m are theoretical values calculated from ν1m, ν2m by Equations (11) and (14) refer to Kimura et al. [17]. ||V||_e, φ_e and ρ_e are experimental values measured from encoder. ν1e, ν2e are experimental values calculated from ||V||_e, φ_e and ρ_e by Equation (22) refer to Kimura et al. [17].

α	0°	10°	20°	30°
||V|| (m/s)	1	0.98	0.93	0.84
φ (°)	−90	−90	−90	−90
ρ (°)	0	0	0	0

Table 2

Values calculated from v₁, v₂ = −0.91 (m/s)

3.1.1. Inverse kinematics

Figures 4–7 exhibit the theoretical data ν1m, ν2m and experimental data ν1e, ν2e. And, Tables 3–6 show the absolute mean error calculated in interval of 7–8 (s). We consider comparison between ν1m, ν2m and ν1e, ν2e in detail, see below.

Figure 4

Comparison theoretical value ν1m and experimental value in α = 0°.

Figure 5

Comparison theoretical value and experimental value in α = 10°.

Figure 6

Comparison theoretical value and experimental value in α = 20°.

Figure 7

Comparison theoretical value and experimental value in α = 30°.

	1	2	3	4	5
|ν1m−ν1e| (m/s)	0.03	0.04	0.10	0.10	0.03
|ν2m−ν2e| (m/s)	0.03	0.04	0.02	0.04	0.04

Table 3

Absolute mean error [7–8 (s)] in α = 0°

	1	2	3	4	5
|ν1m−ν1e| (m/s)	0.04	0.03	0.08	0.03	0.02
|ν2m−ν2e| (m/s)	0.03	0.04	0.01	0.04	0.04

Table 4

Absolute mean error [7–8 (s)] case of α = 10°

	1	2	3	4	5
|ν1m−ν1e| (m/s)	0.05	0.05	0.06	0.09	0.07
|ν2m−ν2e| (m/s)	0.03	0.03	0.05	0.06	0.05

Table 5

Absolute mean error [7–8 (s)] case of α = 20°

	1
|ν1m−ν1e| (m/s)	0.08
|ν2m−ν2e| (m/s)	0.05

Table 6

Absolute mean error [7–8 (s)] case of α = 30°

In the evaluation case of α = 0°, ν1e and ν2e are close to ν1m and ν2m, respectively (see Figure 4). As shown in Table 3, |ν1m−ν1e| is almost 0.04 (m/s), |ν2m−ν2e| is 0.04 (m/s).

In the evaluation case of α = 10°, ν1e and ν2e are close to ν1m and ν2m, respectively (see Figure 5). As shown in Table 4, |ν1m−ν1e| is almost 0.04 (m/s), |ν2m−ν2e| is 0.04 (m/s).

In the evaluation case of α = 20°, ν1e and ν2e are close to ν1m and ν2m, respectively (see Figure 6). As shown in Table 5, |ν1m−ν1e| is 0.09 (m/s), |ν2m−ν2e| is 0.06 (m/s).

In the evaluation case of α = 30°, the limitations of the motor drivers and intense dynamical friction that caused heat between the roller surfaces and the sphere obliged us to cease the second and subsequent experiments. However, ||V||_e, φ_e and ρ_e are partially close to ||V||_m, φ_m and ρ_m, respectively (see Figure 7). And, |ν1m−ν1e| is 0.08 (m/s), |ν2m−ν2e| is 0.05 (m/s) (see Table 6).

Thus, inverse kinematics is validated.

3.1.2. Forward kinematics

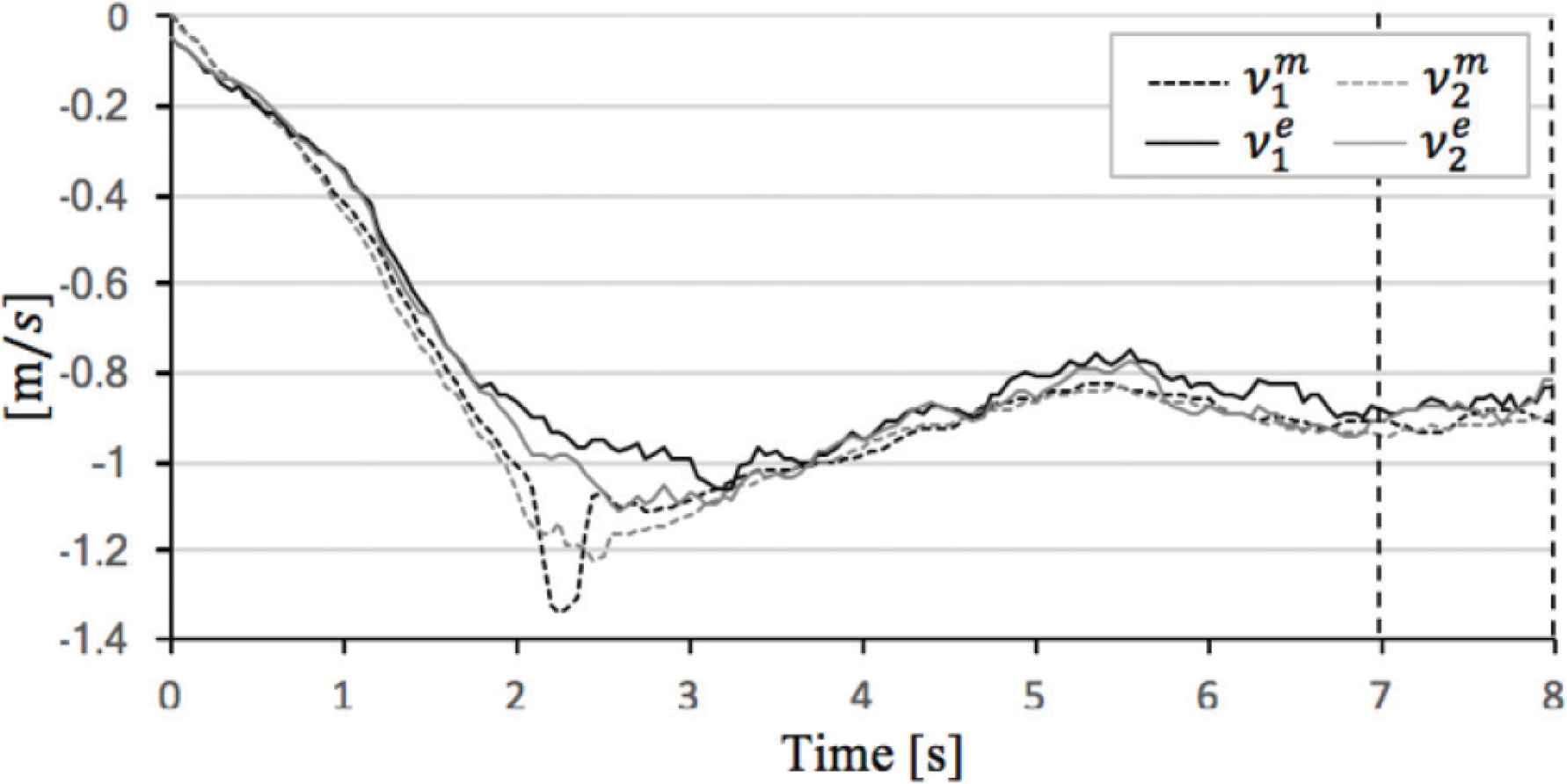
Figures 8–11 exhibit the theoretical data ||V||_m, φ_m, ρ_m and experimental data ||V||_e, φ_e, ρ_e. And, Tables 7–10 show the absolute mean error calculated in interval of 7–8 (s). We consider comparison between ||V||_m, φ_m, ρ_m and ||V||_e, φ_e, ρ_e, respectively in detail, see below.

Figure 8

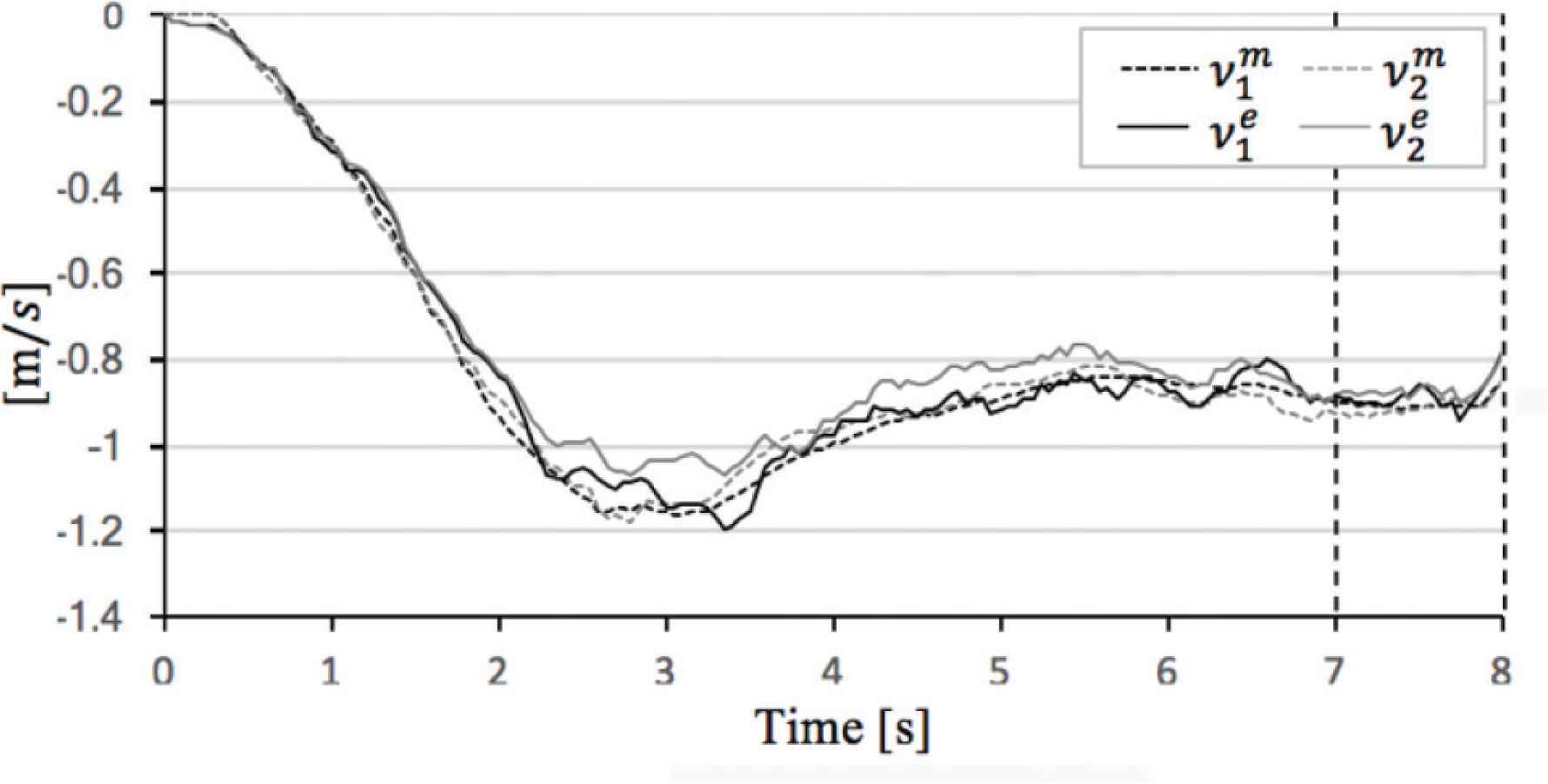
Comparison theoretical value and experimental value in α = 0°. (a) Sphere mobile speed. (b) Sphere direction and angle of sphere rotational axis.

Figure 9

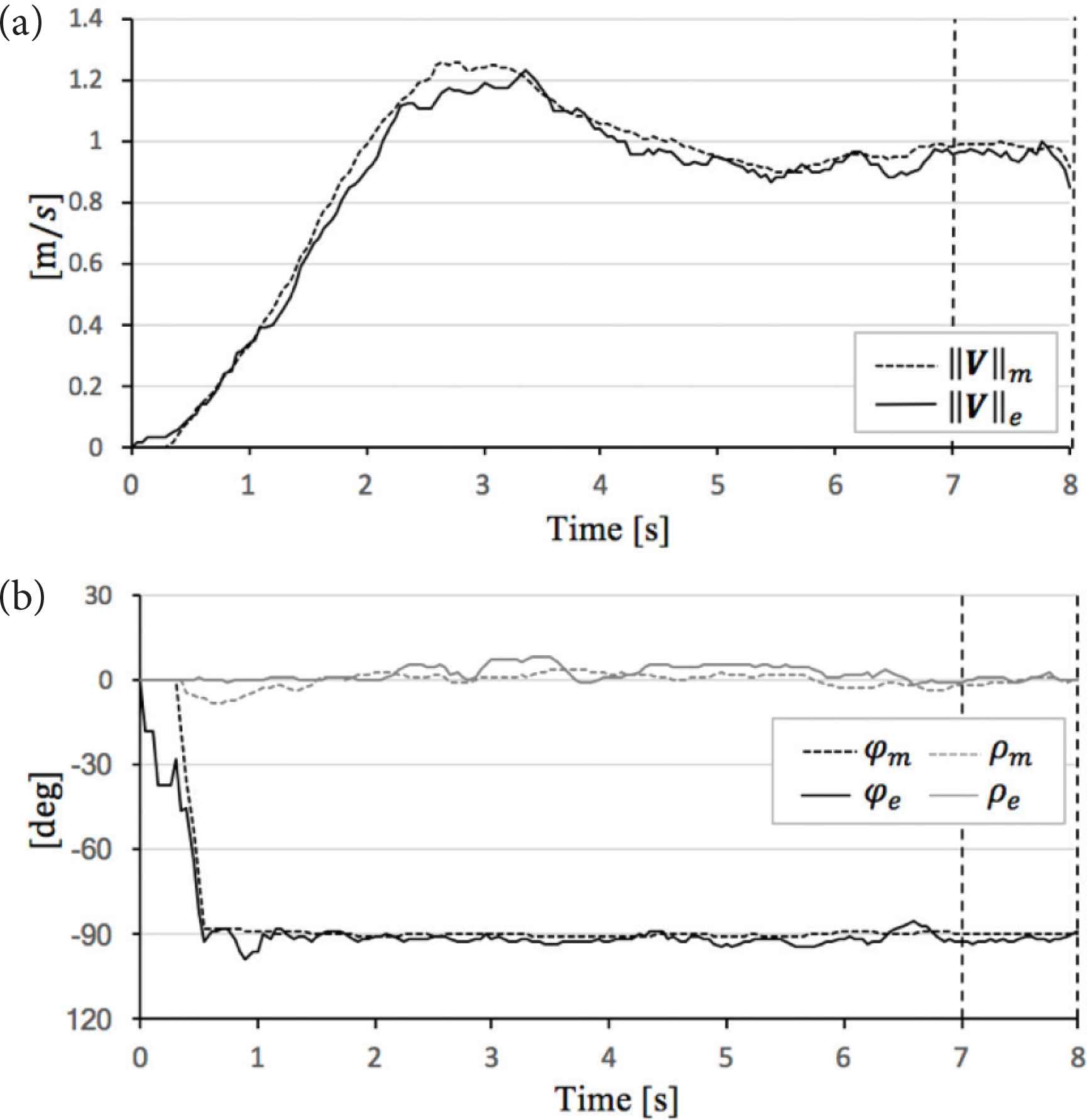
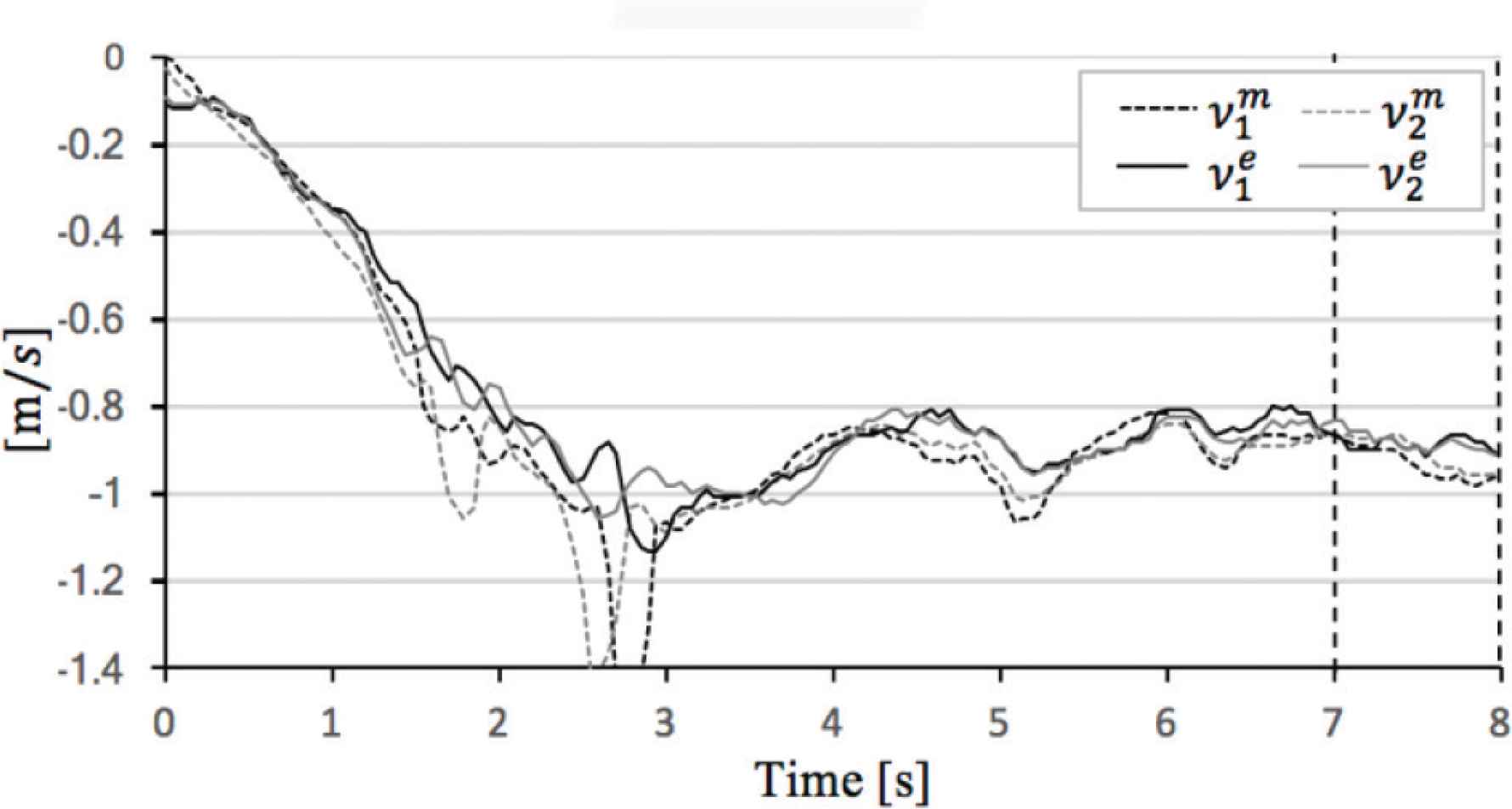
Comparison theoretical value and experimental value in α = 10°. (a) Sphere mobile speed. (b) Sphere direction and angle of sphere rotational axis.

Figure 10

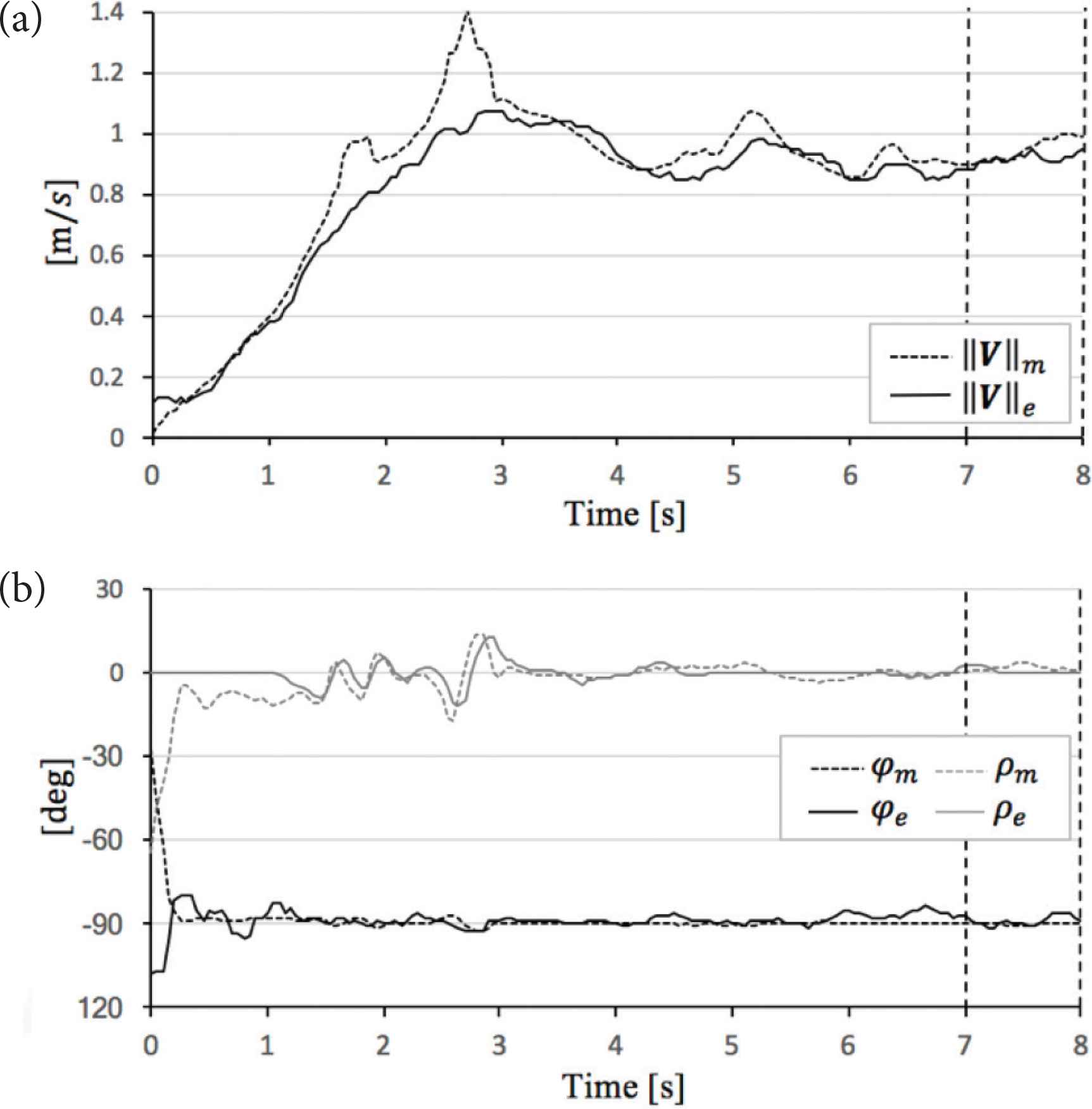
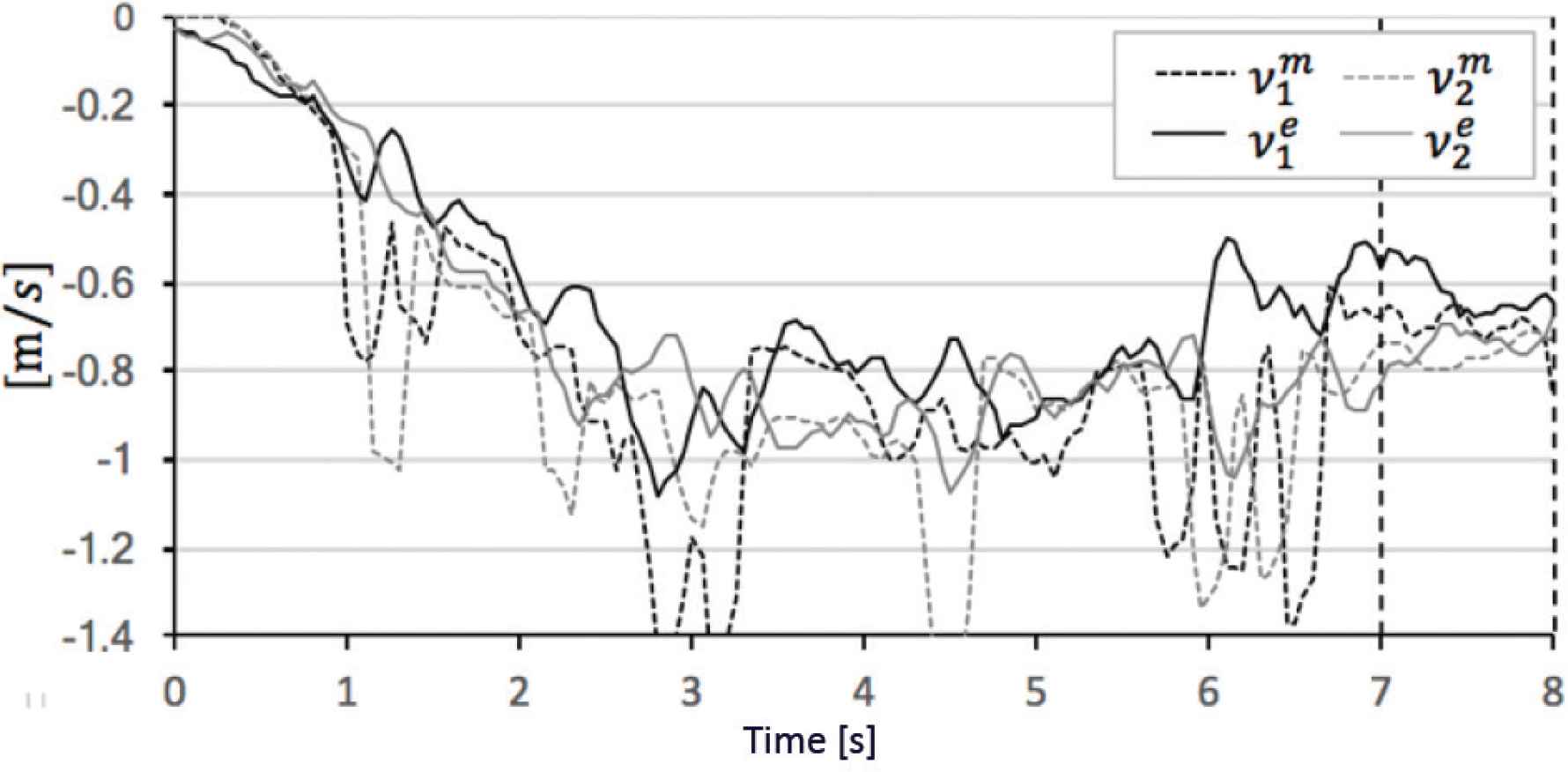
Comparison theoretical value and experimental value in α = 20°. (a) Sphere mobile speed. (b) Sphere direction and angle of sphere rotational axis.

Figure 11

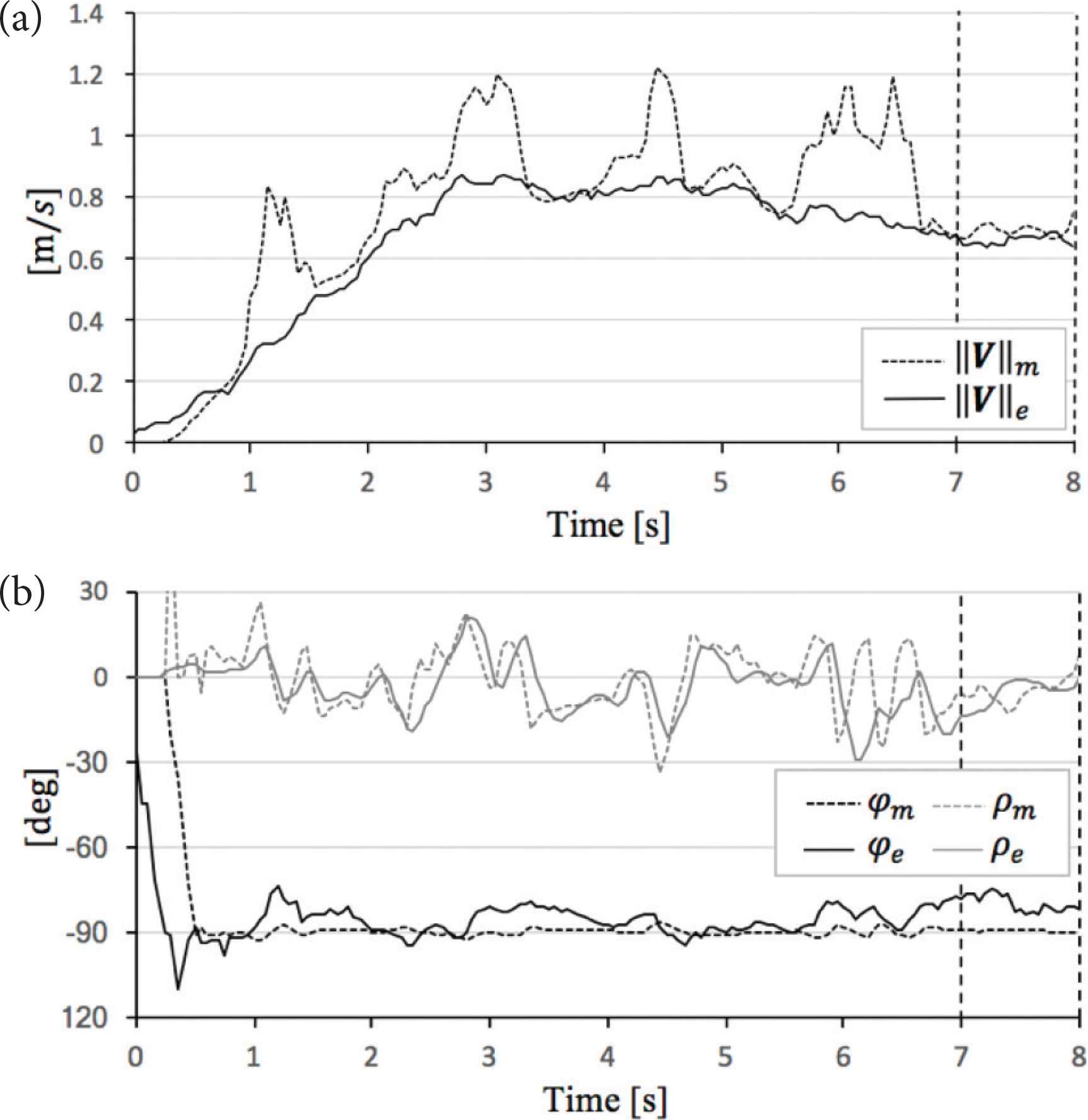
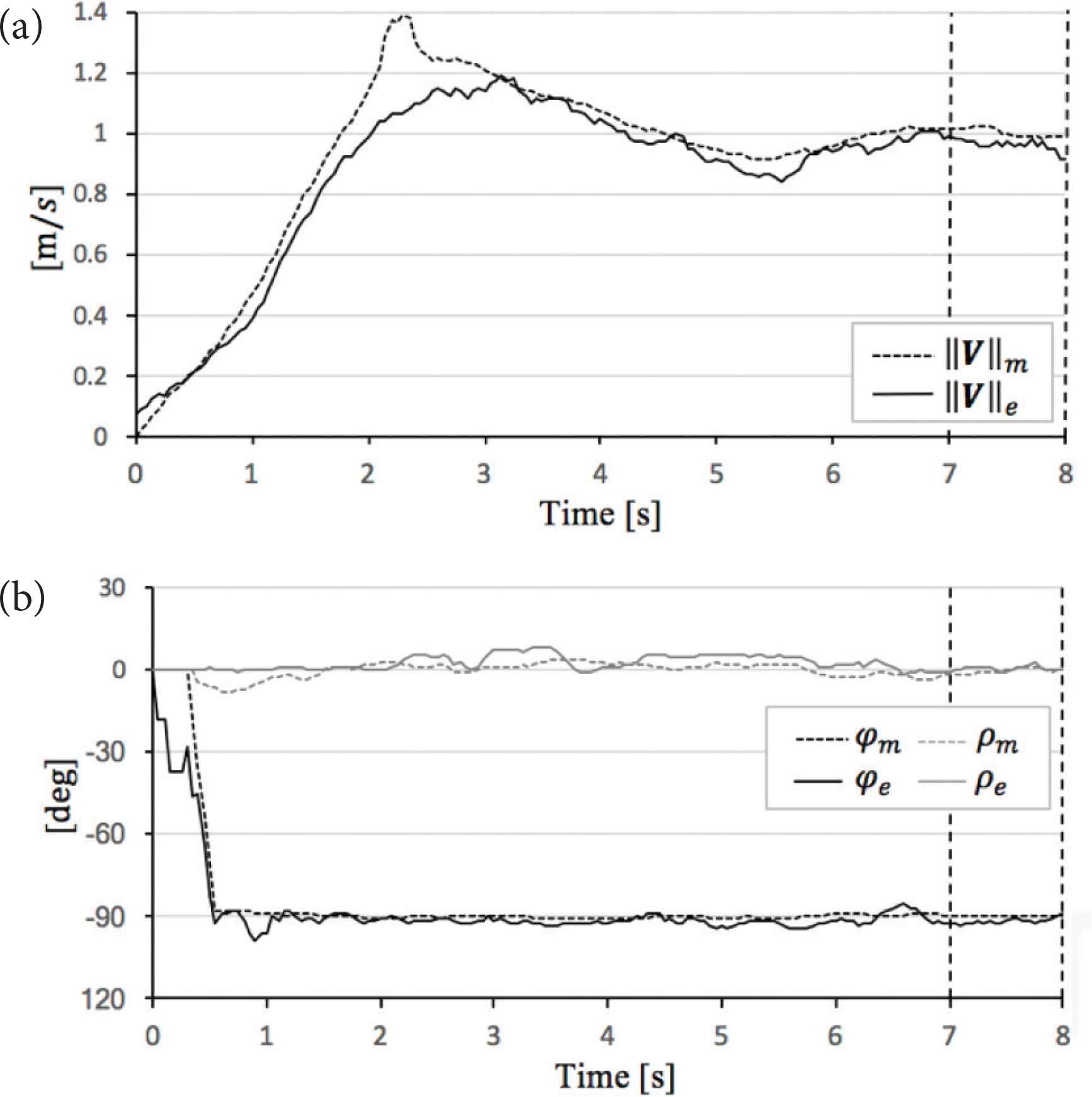
Comparison theoretical value and experimental value in α = 30°. (a) Sphere mobile speed. (b) Sphere direction and angle of sphere rotational axis.

	1	2	3	4	5
|||V||m − ||V||e| (m/s)	0.03	0.04	0.05	0.06	0.04
|φm − φe| (°)	1.5	1.6	2.2	3.9	0.8
|ρm − ρe| (°)	0.7	0.9	6.3	5.3	0.9

Table 7

Absolute mean error [7–8 (s)] in α = 0°

	1	2	3	4	5
|||V||m − ||V||e| (m/s)	0.03	0.04	0.04	0.03	0.03
|φm − φe| (°)	1.2	1.8	3.1	2.2	2.0
|ρm − ρe| (°)	2.1	1.0	3.9	1.2	1.2

Table 8

Absolute mean error [7–8 (s)] in α = 10°

	1	2	3	4	5
|||V||m − ||V||e| (m/s)	0.03	0.03	0.06	0.07	0.05
|φm − φe| (°)	1.5	2.3	2.7	2.7	4.3
|ρm − ρe| (°)	1.9	1.4	2.1	2.1	2.1

Table 9

Absolute mean error [7–8 (s)] in α = 20°

	1
|||V||m − ||V||e| (m/s)	0.04
|φm − φe| (°)	9.7
|ρm − ρe| (°)	5.1

Table 10

Absolute mean error [7–8 (s)] in α = 30°

α	0°	10°	20°	30°
S1 (m/s)	0	−0.16	−0.31	−0.45
T1 (m/s)	0	0	0	0
S2(m/s)	0	0.16	0.31	0.45
T2 (m/s)	0	0	0	0

Table 11

Values calculated from v₁, v₂ = −0.91 (m/s)

In the evaluation case of α = 0°, ||V||_e, φ_e and ρ_e are close to ||V||_m, φ_m and ρ_m, respectively (see Figure 8). As shown in Table 7, |||V||_m − ||V||_e| is 0.06 (m/s), |φ_m − φ_e| is 3.9 (°), and |ρ_m − ρ_e| is 6.3 (°).

In the evaluation case of α = 10°, ||V||_e, φ_e and ρ_e are close to ||V||_m, φ_m and ρ_m (see Figure 9). As shown in Table 8, |||V||_m − ||V||_e| is 0.04 (m/s), |φ_m − φ_e| is 3.1 (°), and |ρ_m − ρ_e| is 3.9 (°).

In the evaluation case of α = 20°, ||V||_e, φ_e and ρ_e are close to ||V||_m, φ_m and ρ_m, respectively (see Figure 10). As shown in Table 9, |||V||_m − ||V||_e| is 0.07 (m/s), |φ_m − φ_e| is 4.3 (°), and |ρ_m − ρ_e| is 2.1 (°).

In the evaluation case of α = 30°, the data have intense behavior due to limitations of the motor drivers. However, ||V||_e, φ_e and ρ_e are partially close to ||V||_m, φ_m and ρ_m, respectively (see Figure 11). And, |||V||_m − ||V||_e| is 0.04 (m/s), |φ_m − φ_e| is 9.7 (°), and |ρ_m − ρ_e| is 5.1 (°) (see Table 10).

Thus, forward kinematics is validated.

3.2. Consideration of Slip Velocity Vector

As shown in Table 11, S_i (i = 1, 2) are values calculated from v₁, v₂ = −0.91 (m/s) by Equation (1). Sim (i = 1, 2) are theoretical values calculated from ν1m and ν2m by Equation (1). Sie and Tie (i = 1, 2) are experimental values calculated from ||V||_e, φ_e, ρ_e, ν1e and ν2e by Equations (1) and (2).

Using Equation (2) as νi=νim(i=1,2), we give Tim=0 (i = 1, 2). And, as νi=νie(i=1,2), we give Tie=0 (i = 1, 2). Thus, ||Tim|−|Tie||=0 and, ζ₁ and ζ₂ are correspond to tangent vectors on a great circle C_G.

Figures 12–15 exhibit the theoretical data Sim (i = 1, 2) and experimental data Sie (i = 1, 2). And, Tables 12–15 show the absolute mean error [calculated in interval of 7–8 (s)]. We consider comparison between Sim (i = 1, 2) and Sie (i = 1, 2) in detail, see below.

Figure 12

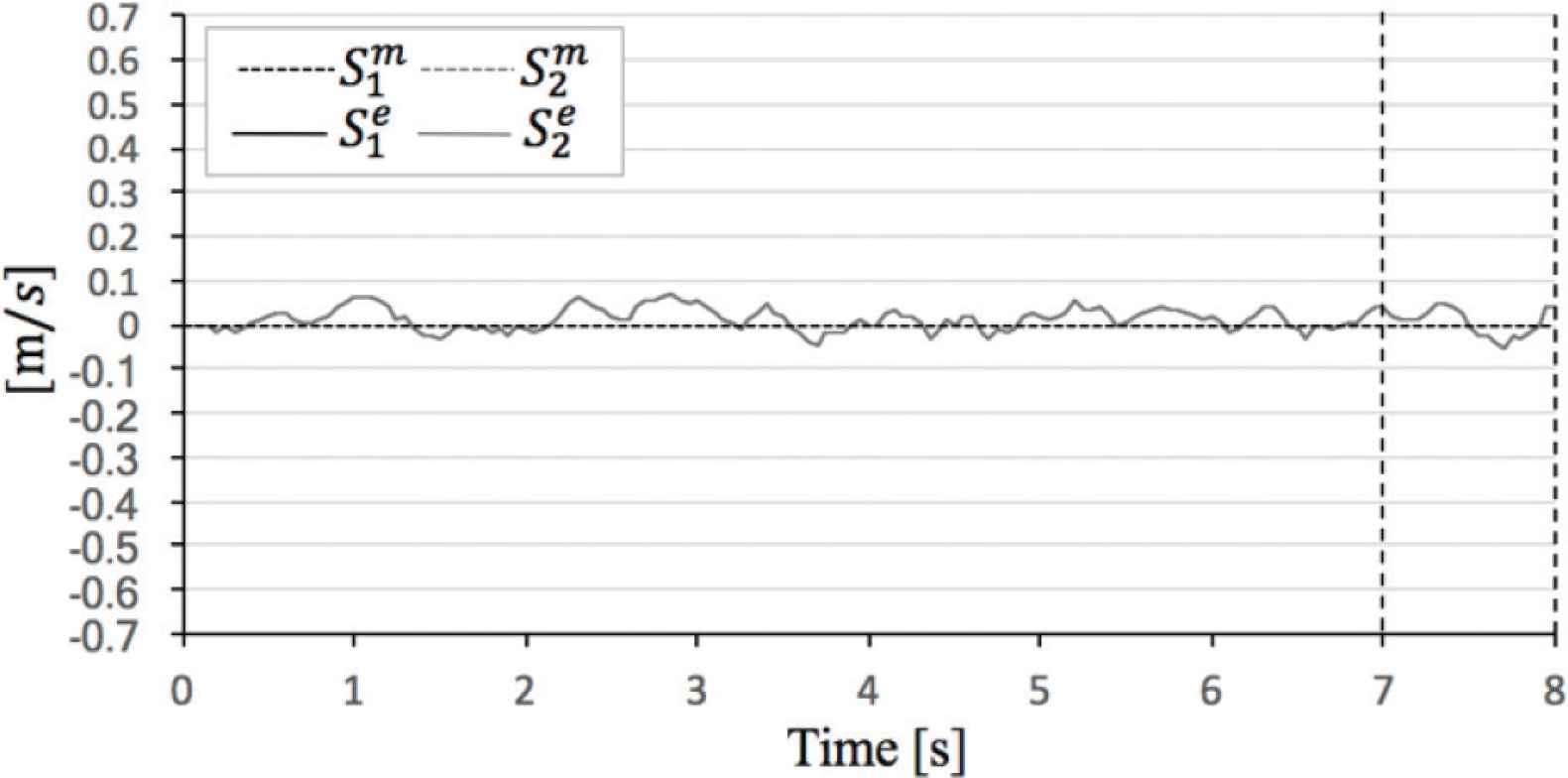
Comparison theoretical value and experimental value in α = 0°.

Figure 13

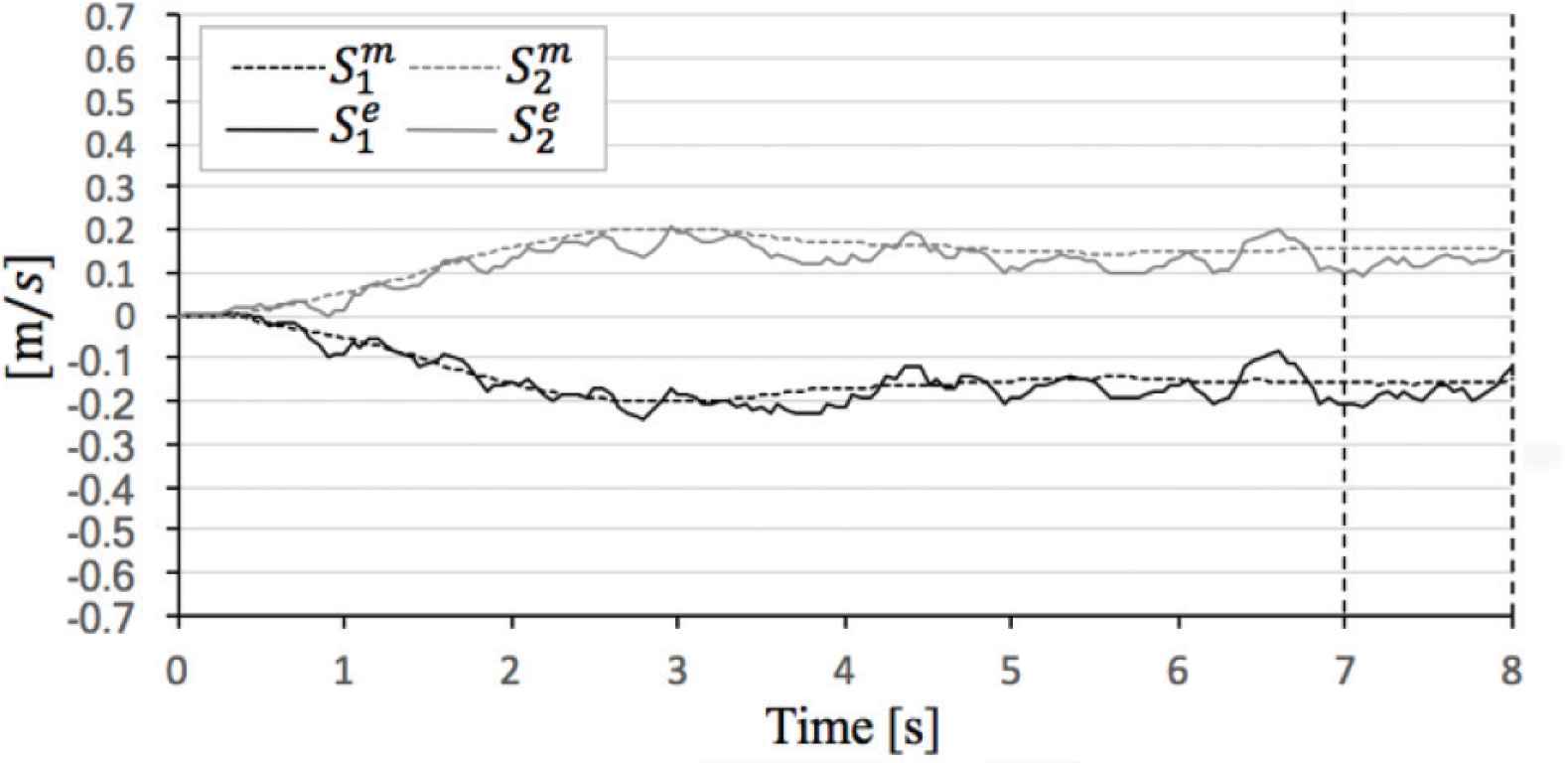
Comparison theoretical value and experimental value in α = 10°.

Figure 14

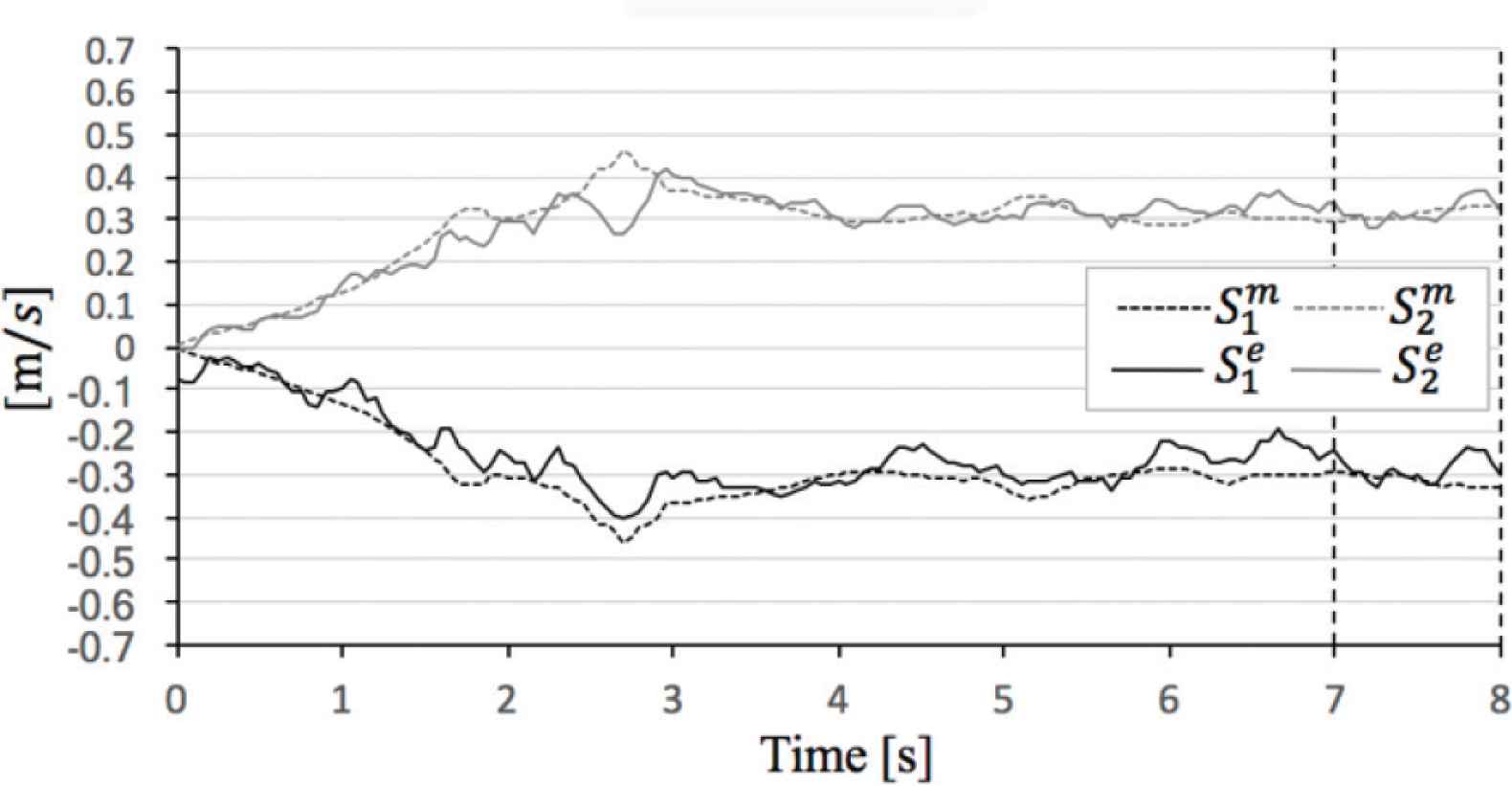
Comparison theoretical value and experimental value in α = 20°.

Figure 15

Comparison theoretical value and experimental value in α = 30°.

	1	2	3	4	5
|S1m−S1e| (m/s)	0.02	0.03	0.02	0.04	0.01
|S2m−S2e| (m/s)	0.02	0.03	0.02	0.04	0.01

Table 12

Absolute mean error [7–8 (s)] in α = 0°

	1	2	3	4	5
|S1m−S1e| (m/s)	0.02	0.03	0.04	0.03	0.03
|S2m−S2e| (m/s)	0.02	0.03	0.03	0.04	0.03

Table 13

Absolute mean error [7–8 (s)] in α = 10°

	1	2	3	4	5
|S1m−S1e| (m/s)	0.03	0.04	0.06	0.05	0.09
|S2m−S2e| (m/s)	0.02	0.03	0.02	0.03	0.05

Table 14

Absolute mean error [7–8 (s)] in α = 20°

	1
|S1m−S1e| (m/s)	0.13
|S2m−S2e| (m/s)	0.08

Table 15

Absolute mean error [7–8 (s)] in α = 30°

In the evaluation case of α = 0°, S1e and S2e are close to S1m and S2m, respectively (see Figure 12). As shown in Table 12, ||S1m|−|S1e|| is 0.04 (m/s) and ||S2m|−|S2e|| is 0.04 (m/s).

In the evaluation case of α = 10°, S1e and S2e are close to S1m and S2m, respectively (see Figure 13). As shown in Table 13, ||S1m|−|S1e|| is 0.04 (m/s) and ||S2m|−|S2e|| is 0.04 (m/s).

In the evaluation case of α = 20°, S1e and S2e are close to S1m and S2m, respectively (see Figure 14). As shown in Table 14, ||S1m|−|S1e|| is 0.09 (m/s) and ||S2m|−|S2e|| is 0.05 (m/s).

In the evaluation case of α = 30°, the data have intense behavior due to limitations of the motor drivers. However, S1e and S2e are partially close to S1m and S2m, respectively (see Figure 15). And, ||S1m|−|S1e|| is 0.13 (m/s) and ||S2m|−|S2e|| is 0.08 (m/s) (see Table 15).

Thus, Equations (1)–(3) is validated by experiment.

4. CONSIDERATION OF WORLD TEAMS’ ROLLERS ARRANGEMENT

Figure 16 shows the relationship between the sphere slip speed and sphere mobile speed. The horizontal and vertical axes show Sie (i = 1, 2) and ||V||_e, respectively.

Figure 16

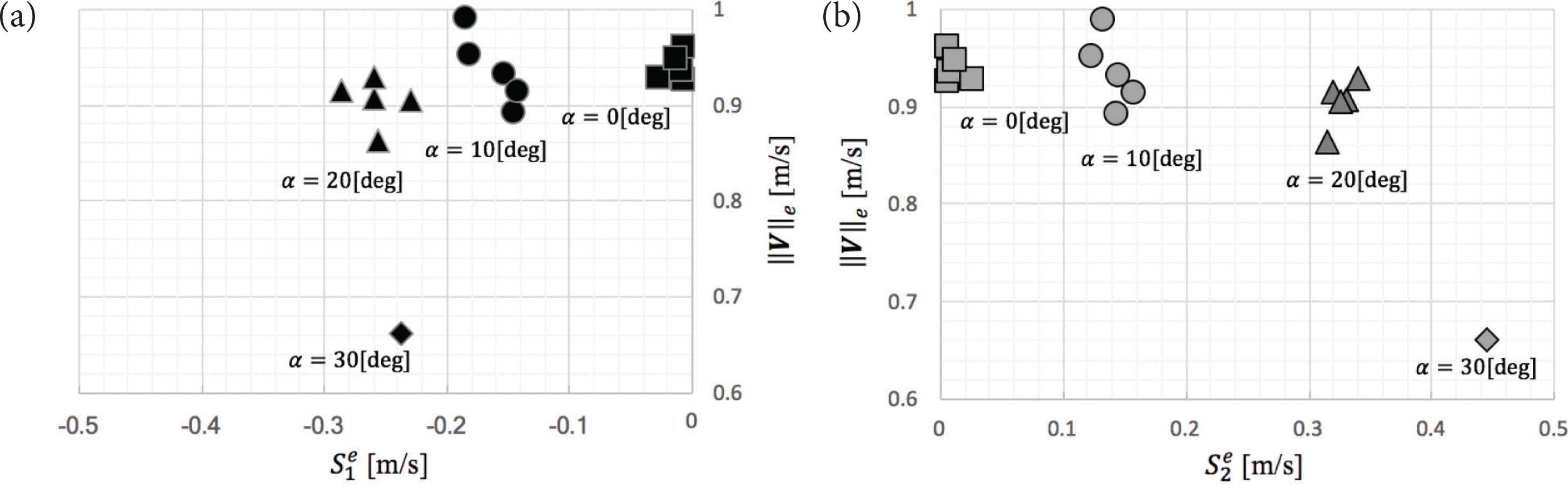
Relationship between sphere slip speed and sphere mobile speed. (a) Left-side roller. (b) Right-side roller.

The configurations (left-side roller) and (right-side roller) indicate the coordinates [S1e,‖V‖e]T and [S2e,‖V‖e]T, respectively, corresponding to the experimental mean values calculated over intervals of 7–8 (s).

5. CONCLUSION

In this study, we verified derive the sphere kinematics that allows for slipping and considered sphere slip velocity vector and evaluated the roller arrangement used by the world teams. As a result, Tech United Turtles and Falcons have adopted optimum roller arrangement in teams of mobile speed efficiency.

In future studies, by applying the ball-dribbling mechanism, this model should be verified experimentally.

CONFLICTS OF INTEREST

The authors declare they have no conflicts of interest.

Authors Introduction

Mr. Kenji Kimura

He received the ME (mathematics) from Kyusyu University in 2002. Then he was a mathematical teacher and involved in career guidance in high school up to 2014. Currently, he is an educator of International Baccalaureate Diploma Program (Mathematics: applications and interpretation, analysis and approaches) in Fukuoka Daiichi High School, and student in the doctoral program of the Kyushu Institute of Technology. His current research interests are spherical mobile robot kinematics, control for object manipulation.

Dr. Shota Chikushi

He received the M.S. and D.S. degrees from the Department of Life Science and Systems Engineering, Kyushu Institute of Technology, Fukuoka, Japan, in 2012 and 2018, respectively. He is an Assistant professor in the Department of Precision Engineering, Graduate School of Engineering, University of Tokyo. From 2015 to 2018, he was an Assistant professor of the Nippon Bunri University, Oita, Japan. His research interests are motion control of a roller-driven sphere, design for autonomous omnidirectional mobile robot and operation support of disaster response robot in unmanned construction.

Dr. Kazuo Ishii

He is a Professor in the Kyushu Institute of Technology, where he has been since 1996. He received his PhD degree in Engineering from University of Tokyo, Tokyo, Japan, in 1996. His research interests span both Ship Marine Engineering and Intelligent Mechanics. He holds five patents derived from his research. His lab got “Robo Cup 2011 Middle Size League Technical Challenge 1st Place” in 2011. He is a member of the Institute of Electrical and Electronics Engineers, the Japan Society of Mechanical Engineers, Robotics Society of Japan, the Society of Instrument and Control Engineers and so on