Journal of Robotics, Networking and Artificial Life

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 5, Issue 4, March 2019, Pages 273 - 277

Quantitative Evaluation in Discrete-time Domain and Improvement in Intersample Response on Multirate Optimal Control

Authors
Takao Sato*, Natsuki Kawaguchi, Nozomu Araki, Yasuo Konishi
Graduate School of Engineering, University of Hyogo, Himeji, Hyogo, 671-2280, Japan
*Corresponding author. Email: tsato@eng.u-hyogo.ac.jp
Corresponding Author
Takao Sato
Received 22 October 2018, Accepted 20 November 2018, Available Online 30 March 2019.
DOI
10.2991/jrnal.k.190220.015How to use a DOI?
Keywords
Sampled-data control system; dual-rate system; intersample response; discrete-time response; null-space; redundancy
Abstract

In this study, the dual-rate sampled-data control system is designed, where the sampling interval of a plant output is an integer multiple of the holding interval of a control input. Because the discrete-time Linear Quadratic Integrator (LQI) is used for optimizing the discrete-time control performance, intersample output might oscillate. To eliminate the oscillation of the intersample ripple caused by the input oscillation, the designed LQI controller is extended. Finally, the original LQI control law and the extended control laws are quantitatively compared.

Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

Most recent control systems are implemented using the discrete-time digital computer. On the other hand, the controlled object is not only a discrete-time system but also a continuous-time system. When the continuous-time system is controlled using the digital computer, such a control system is called sampled-data control system [1]. In the single-input/-output system, there are two intervals: the holding interval of a control input and the sampling interval of a plant output. This study discusses a design method for controlling a dual-rate control system, where the sampling interval is longer than the holding interval.

In such a dual-rate control system, intersample ripples might occur even if the sampled output converges to the reference input because the control input can be changed between the sampling intervals [2]. Therefore, the condition for eliminating the intersample ripples caused by the input oscillation has been proposed [3].

This study proposes two design methods for eliminating the intersample ripples: one is an extension method based on the null-space [4], and the other is to weight on the input deviation. When the intersample response is improved, the discrete-time sampled response might be degraded, and hence the performance degradation should be fairly evaluated. The extension method using the null-space has been proposed [5,6]. The conventional method [5] is derived using the polynomial approach, whereas the proposed method is designed based on the state-space representation. As a state-space approach, the conventional method [6] is designed using the null-space. However, because the integral compensation is not included, the robust-tracking for the step-type reference input or the step-type disturbance is not achieved. On the other hand, a state-space design method using the integral compensation has been proposed [7]. In this method, the intersample ripples are eliminated. However, an existing discrete-time response is not maintained because the null-space is not used. Finally, the effectiveness of the proposed method is demonstrated through numerical examples, and the control performances are quantitatively evaluated based on the numerical results. Furthermore, this study shows that the discrete-time performance of the state variable is not changed using the extension method using the null-space.

2. CONTROLLED PLANT MODEL

A controlled plant is an unknown linear continuous-time single- input and -output time-invariant system given as the following Equations (1) and (2):

x˙(t)=Acx(t)+bcu(t)
y(t)=ccTx(t)
where x(t) ∈ Rn is the state variable, u(t) ∈ R is the control input, and y(t) ∈ R is the plant output, respectively. Ac ∈ Rn×n is a coefficient matrix, and bc ∈ Rn and cc ∈ Rn are coefficient vectors. Because the sampled-data control system is designed, a continuous-time plant output is sampled, and a discrete-time control input is held. Since the sampling interval of the plant output is an integer multiple of the holding interval of the control input, the following lifted dual-rate model is obtained [Equations (3)–(5)].
x(k+l)=Alx(k)+Blu(k)
u(k)=[u(k)⋯u(k+l-1)]T
y(k)=clTx(k)
where l is a positive integer. The dual-rate model is assumed to be known, and a sampled-data control system is designed based on this model. It is assumed that (Al, Bl) is stable.

3. OPTIMAL CONTROLLER DESIGN

The control system is designed using the following state feedback control law [Equations (6)–(8)]:

u(k)=-Fz(k)
z(k)=[x(k)xi(k)]T
xi(k+l)=xi(k)+(r(k)-y(k))Ts
where r(k) ∈ R is the reference input to be followed by the plant output, and Ts denotes the sampling interval of the plant output. F ∈ Rl×(n+1) is the feedback gain, and it is designed using the Linear Quadratic Integrator (LQI) [Equation (9)] [8]:
J=∑k=0∞(z(k)TQz(k)+u(k)TRu(k))
where Q ∈ R(n+1)×(n+1) is a positive definite matrix, and R ∈ Rl×l is a positive semi-definite matrix. The performance index is rewritten as the following Equations (10)–(12):
J=Jz+Ju
Jz=∑k=0∞z(k)TQz(k)
Ju=∑k=0∞u(k)TRu(k)

The closed-loop system using control law (6) is obtained as follows:

z(k+l)=(Az-BzF)z(k)+Er(k)
Az=[Al0-TscT1],  Bz=[Bl01×l],  E=[0n×1Ts]

4. TWO INTERSAMPLE SUPPRESSION METHODS

To eliminate the intersample ripples caused by the input oscillation between the sampling instants, two extension methods are proposed.

4.1. Null-space Method

One extension method is based on the null-space.

B⊥ ∈ Rl×(l–1) is defined as the following Equations (15) and (16):

Im(B⊥)=Ker(Bl)
Ker(Bl)={b⊥∈Rl|Blb⊥=0n,1,b⊥≠0}

Using the defined B⊥, the control law is extended as follows:

u(k)=-Fx(k)+B⊥w(k)
where w(k) ∈ Rl−1 is a newly introduced vector.

The closed-loop system using the extended control law (11) is obtained as follows:

z(k+l)=(Az-BzF)x(k)+Er(k)+BzB⊥w(k)

From the definition of B⊥, the last-term in the right-hand side of Equation (18) is 0(n+1)×1. As a result, the closed-loop system is not affected by w(k). In this study, w(k) is designed so that all the elements in u(k) are equivalent.

4.2. Input-weighting Method

In the other extension method, the deviation of the control input is suppressed in LQI. To this end, the difference between u(k + i) and u(k + i + 1) is penalized as the following Equations (19) and (20):

δi(u(k+i-1)-u(k+i))2=[u(k+i-1)u(k+i)]Δi[u(k+i-1)u(k+i)]
Δi=δi[1-1-11]
where δi ∈ R is a non-negative weighting factor. To evaluate the weighted input deviation in LQI, Ju in Equation (12) is replaced with the following criterion (21):
Ju=∑k=0∞u(k)T(R+Δ)u(k)
where Δ is a matrix which satisfies Equation (22):
∑i=1l-1δi(u(k+i-1)-u(k+i))2=u(k)TΔu(k)

In the proposed weighting method, Ju must be redesigned. Therefore, the Riccati equation is resolved by replacing Equation (12) by Equation (21).

5. DISCUSSION ON DISCRETE-TIME AND INTERSAMPLE CONTROL PERFORMANCE

In the dual-rate sampled-data control system, the discrete-time model is available, and the continuous-time model is not always obtained. In such a case, when the discrete-time performance is optimized, the intersample ripples might be caused by the input deviation between the sampling instants, although the discrete-time performance is optimized.

In this study, the discrete-time performance is optimized based on the known lifted dual-rate model, and the designed control law is extended so that the intersample performance is improved. In the discrete-time performance evaluation, because the discrete-time performance function consists of Jx and Ju, two indices are quantitatively evaluated.

In the first extension method based on the null-space, the intersample ripples can be eliminated by introducing the new design parameter. Further, the parameter is designed independent of the discrete-time closed-loop system. Therefore, Jx is maintained and Ju is changed. Hence, the optimization on the control input is not maintained.

In the second extension method, since the difference of the control input is always penalized, the input deviation is suppressed. As a result, the intersample ripples caused by the input deviation is eliminated. However, both Jx and Ju are affected by the weighting factor δi.

6. NUMERICAL EXAMPLE

Consider a continuous-time system given as the following Equation (23):

G(s)=13s+1

The sampling interval and the holding interval are 2s and 1s, respectively, and the following lifted dual-rate system is given as Equations (24) and (25):

x(k+2)=0.51x(k)+[0.721.0]u(k)
y(k)=0.28x(k)

The feedback gain is obtained by solving the LQI problem with Q = R = I2. The reference input is a unit step function.

The control result using the original feedback control law (6) is shown in Figure 1. This figure shows that the sampled output converges to the reference input at the sampling instants. However, the control input oscillates, and the intersample output hence oscillates. In the LQI design, the amount of the control input is evaluated, but the intersample output is not evaluated. Therefore, the deviation of the control input is not attenuated, and the intersample ripples occur.

Figure 1

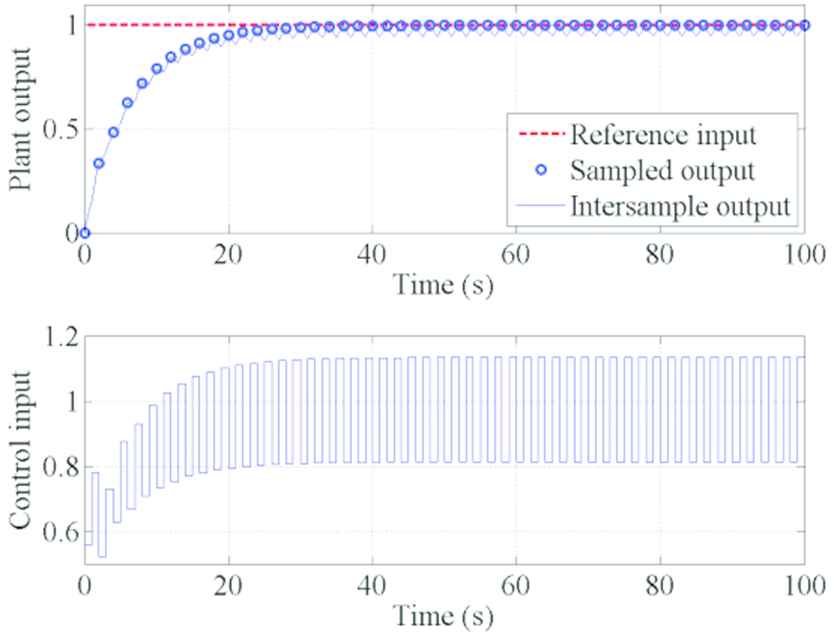
Simulation result using the original state feedback control law (upper: output trajectory, lower: input trajectory).

To eliminate the intersample ripples caused by the input deviation, the extended controllers are applied. The result using the extended controller designed in Subsection 4.1 is shown in Figure 2. The lower figure shows that the control input is constant between the sampling instants, and the upper figure shows that the intersample ripples are eliminated. Furthermore, the sampled output response is the same as Figure 1 even though the control input is redesigned.

Figure 2

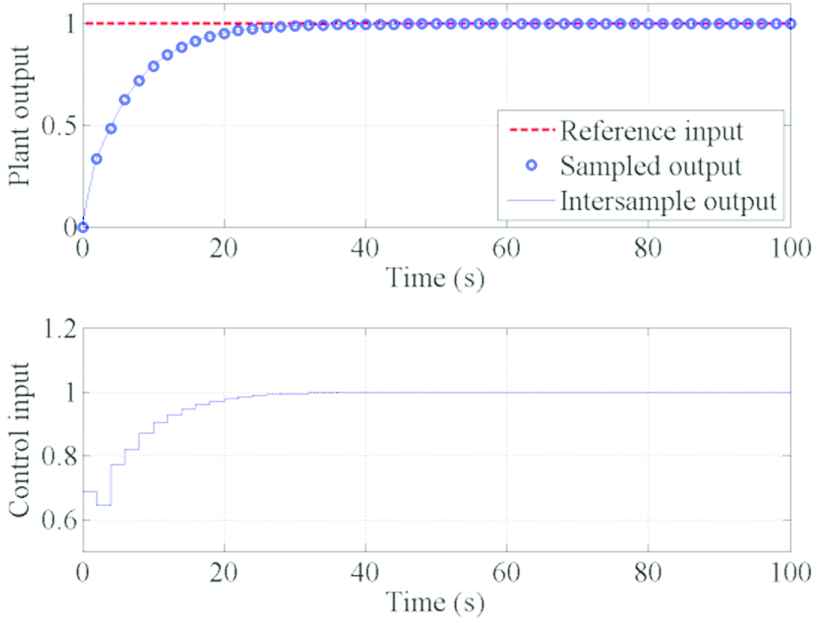
Simulation result using the extended method is given in Subsection 4.1.

The control results using the extended controller designed in Subsection 4.2 are shown in Figures 3 and 4, where δ1 is set to 100 and 105, respectively. In both figures, the amplitude of the difference in the control input is attenuated since the control input deviation between the sampling instants is penalized. The larger δ1, the smaller the amplitude of intersample ripples.

Figure 3

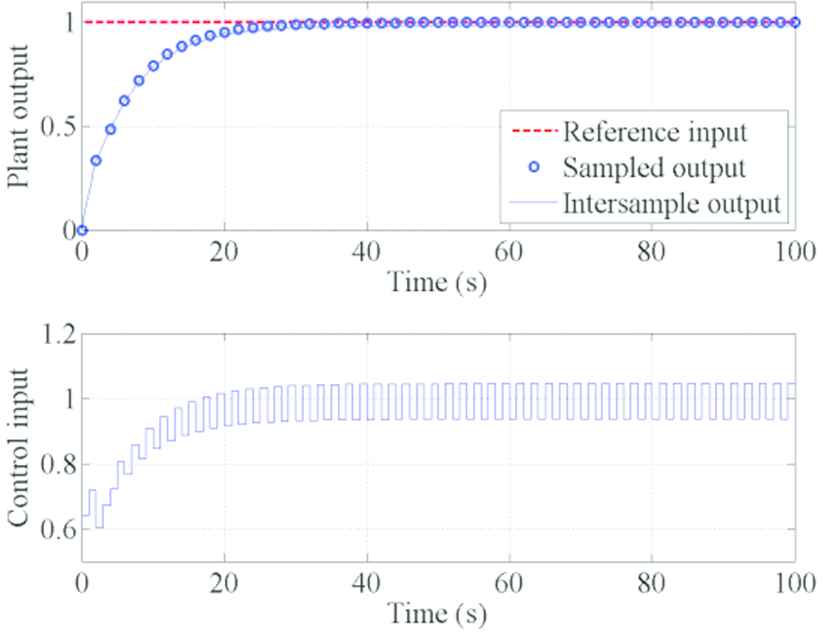
Simulation result using the extended method is given in Subsection 4.2 with δ1 = 100.

Figure 4

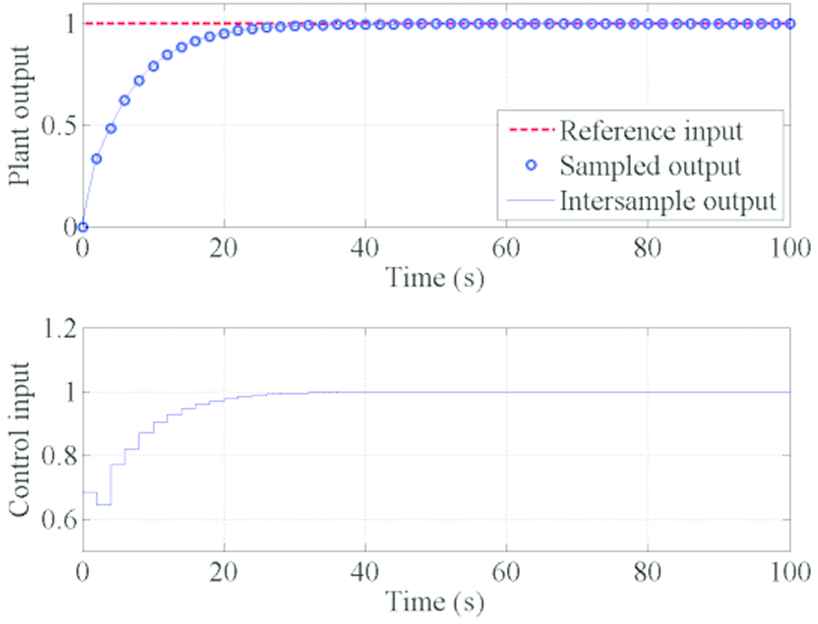
Simulation result using the extended method is given in Subsection 4.2 with δ1 = 105.

For comparing the controllers, the performance indices are quantitatively evaluated in Table 1, where the evaluation length is 50 steps. Table 1 shows that the index J50 of the original LQI is best, and that of the extended methods are increased, although the intersample ripples are suppressed. In the index of state z, Jz50 , the original LQI is best and it is the same as the extended method of Subsection 4.1 because the original closed-loop system is maintained in the extended controller designed in Subsection 4.1.

Controller Jz50(×103) Ju50 J50
Original 3.029 93.82 3.122
4.1 3.029 96.38 3.125
4.2 (δ1 = 100) 3.034 95.49 3.130
4.2 (δ1 = 105) 3.037 96.35 3.133
Table 1

Index values

7. CONCLUSION

This study has discussed the design methods for controlling a dual-rate sampled-data control system. First, an optimal control law is designed using LQI.

Second, the designed control law is extended using two methods: one is based on the null-space, and the other is to weight the input deviation between the sampling instants. At last, the effectiveness of the proposed method is demonstrated through the numerical examples, and the control performances are quantitatively evaluated.

ACKNOWLEDGMENT

This study was supported by JSPS KAKENHI Grant Number 16K06425.

Authors Introduction

Dr. Takao Sato

He received the B. Eng. and M. Eng. degrees from Okayama University, in 1997 and 1999, respectively, and his D. Eng. degree from Okayama University in 2002. He is an associate professor in the Graduate School of Engineering at University of Hyogo. His research interests are in the area of PID control, mechanical system and multirate control. Dr. Sato is a member of the Society of Instrumentation and Control Engineers in Japan (SICE) and the Institute of Systems, Control and Information Engineers in Japan (ISCIE).

Dr. Natsuki Kawaguchi

He received the D. Eng degree from Okayama University in 2018. He is an assistant professor in the Graduate School of Engineering at University of Hyogo. His research interests are in the area of fault detection and fault tolerant control.

Dr. Nozomu Araki

He received his PhD degree from University of Hyogo, Japan in 2007. He is presently working as an Assistant Professor in the Department of Mechanical System, University of Hyogo, Japan. His research interest includes control engineering, signal processing and medical engineering.

Prof. Yasuo Konishi

He received his PhD in mechanical engineering from Keio University, Tokyo, Japan, in 1989. He is a professor at the University of Hyogo, and is presently the head of the Laboratory of Control Engineering. His research focuses on the game-theoretical approach to mechanical design, time optimal control by binary input using MLDS, and positioning control with static and kinetic friction using hybrid controllers.

REFERENCES

[1]T Chen and BA Francis, Optimal sampled-data control systems, Springer-Verlag, London, 1995.
[2]AK Tangirala, D Li, RS Patwardhan, SL Shah, and T Chen, Issues in multirate process control, in Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), IEEE (San Diego, CA, USA, 1999), pp. 2771-2775.
[3]AK Tangirala, D Li, RS Patwardhan, SL Shah, and T Chen, Ripple-free conditions for lifted multirate control systems, Automatica, Vol. 37, 2001, pp. 1637-1645. https://doi.org/10.1016/s0005-1098%2801%2900116-9
[4]L Zaccarian, Dynamic allocation for input redundant control systems, Automatica, Vol. 45, 2009, pp. 1431-1438. https://doi.org/10.1016/j.automatica.2009.01.013
[5]T Sato, N Kawaguchi, N Araki, and Y Konishi, Ripple-free design for an SISO dual-rate control system, in 2017 22nd IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), IEEE (Limassol, Cyprus, 2017). https://doi.org/10.1109/etfa.2017.8247751
[6]R Yasui, N Kawaguchi, T Sato, N Araki, and Y Konishi, State-space design of a dual-rate control system using the null-space, in 2018 International Conference on Information and Communication Technology Robotics (ICT-ROBOT), IEEE (Busan, South Korea, 2018), pp. 1-4. https://doi.org/10.1109/ict-robot.2018.8549914
[7]T Sato, A Yanou, and S Masuda, Ripple-free dual-rate control with two-degree-of-freedom integrator, IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, IEICE Engineeering Science Society, Tokyo, Japan, Vol. E101.A, 2018, pp. 460-466. https://doi.org/10.1587/transfun.e101.a.460
[8]PC Young and JC Willems, An approach to the linear multivariable servomechanism problem, Int. J. Control, Vol. 15, 1972, pp. 961-979. https://doi.org/10.1080/00207177208932211
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Robotics, Networking and Artificial Life
Volume-Issue
5 - 4
Pages
273 - 277
Publication Date
2019/03/30
ISSN (Online)
2352-6386
ISSN (Print)
2405-9021
DOI
10.2991/jrnal.k.190220.015How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Takao Sato
AU  - Natsuki Kawaguchi
AU  - Nozomu Araki
AU  - Yasuo Konishi
PY  - 2019
DA  - 2019/03/30
TI  - Quantitative Evaluation in Discrete-time Domain and Improvement in Intersample Response on Multirate Optimal Control
JO  - Journal of Robotics, Networking and Artificial Life
SP  - 273
EP  - 277
VL  - 5
IS  - 4
SN  - 2352-6386
UR  - https://doi.org/10.2991/jrnal.k.190220.015
DO  - 10.2991/jrnal.k.190220.015
ID  - Sato2019
ER  -