Flock Guiding of Hybrid Agents via Root Block
- DOI
- 10.2991/jrnal.k.190220.008How to use a DOI?
- Keywords
- Flock guiding; matrix block; hybrid order agents; collective behavior
- Abstract
The convergent equilibrium of flocking agents is vital importance for their collective behavior, where flock guiding of hybrid agents, which are composed by both first and second order agents, can only be boiled down to the root node agents, is touched upon here. Both the theoretical analysis and the simulation results are provided to verify the suggested scheme.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The collective behavior of agents has been a long and lasting spotlight in systems and control field. The underpinning knowledge was introduced by Olfati and Murray [1], which including graph theory, adjacent matrix as well as consensus concepts, made clear intuitively. Leader follower agent systems, which have been a focus by many experts, were still being improved up to now. The networks of networks scheme of leader follower systems was made possible by Song et al. [2], which demonstrating interdependence of agents, turned into reality via socialized status of the agents. For the engineering complexity, the agents should be different, and only by this difference, the engineering systems can function well, and in this kind of sense, hybrid agents, especially hybrid agents with heterogenous dynamics, were explored in detail. Hybrid agents with both first and second order dynamics, under auspices of augmented matrix operation [3], could be assumed unified.
In spite of collective behavior of hybrid agents has been explored so deeply, there are still some rooms to be filled in. Among those, the ultimate goal of collective behavior will stand out, for its essential value in the planning of agent goal. Generally speaking, all the members of the agents should contribute and could play their roles, however, counter intuitively, in this paper, in directed networks of hybrid agents, only the root block member agents can dominate the final equilibrium of the flock, this is inevitably innovative for agents flocking. And this finding seems promising in today’s real world, for the authorized agents, their number should be made as less as possible in case of security.
To be distinguished from the already existed results, our points here have at least three standing out viewpoints. At first, block guiding which extends the concept of leader guiding in flocking control has been reported so less often. And secondly, that ultimate goal position is invariant from the leaf block points will be awarded these days for security of the networks. And the third, network of hybrid agents are borrowed to verify the suggested scheme, is much more promising, for the first order agents can be anchor points sometimes and the second order agents can be the mobile agents, which will be guided by the anchor agents.
The structure of this paper is arranged as follows. At first, problem formulation, together with the main results as well as some comments on the main results will be presented in the second part of this paper. Then followed that will be some conclusions, which will be the final part to end up this paper.
2. FLOCK GUIDING OF HYBRID AGENTS
This part will start with the flock guiding of hybrid agents, which will be covered by Subsection 2.1, the theorem will be demonstrated at first, and then some notes about it. Then the main results will be followed at Subsection 2.2, both the topology of the agent networks and the simulation results will be provided, and after that some comments will be made ready to clarify the idea further in Subsection 2.3.
2.1. Problem Formulation
For the directed networks, which is composed of root block nodes and leaf block nodes, will be touched upon here. For the root block nodes, as a whole, they only have output degrees to connect with the other blocks. Intuitively, the nodes of leaf block, as a whole they only have input degrees to connect with the other blocks.
Theorem 1.
Suppose that the coupling matrix A can be turned into the following form:
Proof:
Since ξ is the left Eigen vector corresponding to Eigen value zero of matrix A, then we can get ATξ = 0, and this can be translated into the following Equation (1)
To be concrete, we can have [Equation (2)]
For D is invertible, ξ2 must be zero vector. And in this sense, we can get
Notes: Theorem 1 points out that if sub-matrix A1 has no input degrees and is symmetric, then its corresponding nodes can be named as root nodes and the ultimate state of the networks can be determined by those sub block nodes; if sub matrix D is invertible, and it does not have output degrees connected with the other sub blocks, the nodes corresponding to D can be named as leaf nodes, leaf nodes cannot affect the ultimate state of the networks. So, the definition of root nodes together with leaf nodes is the first requisite for system analysis.
2.2. Main Results
Consider the network, which consists of 5 agents, among which nodes 1 and 2 are root block nodes, while nodes 3–5, are leaf block nodes, this can be referred to Figure 1.

Network consists of five nodes.
To be further, the nodes 1 and 2 are assigned as the first order agents, while nodes 3–5 are assigned as the second order agents, respectively.
The coupling matrix of Figure 1 is easily to be gotten as
The left eigen vector to the zero Eigen value of A is
To be concise, the control action can be expressed as
The introduced control action for agents 1 and 2 are easily to be understood, for agents 1 and 2, they make up of the undirected sub network of root block, and they tend to be convergent to each other, and this convergent and ultimate value will be assigned to the whole agents system further. Control action added for agents 3–5 can make a little nervous at first glimpse, but they still can be made tractable in this way, first we decomposed the added control function into two different parts, and the first part is used to realize the consensus among themselves and their neighbours, and these consensus actions are scaled by proportional factor a, and the second term is velocity damping part, which is also scaled by proportional factor, and the scaled value can be varied from a, and in this case we named the factor as b. The consensus term plus the damping term collaboratively turn the flock guiding of hybrid agents possible. Among which, we assigned a = 1 and b = 2, respectively. The simulation results can be seen in Figure 2.
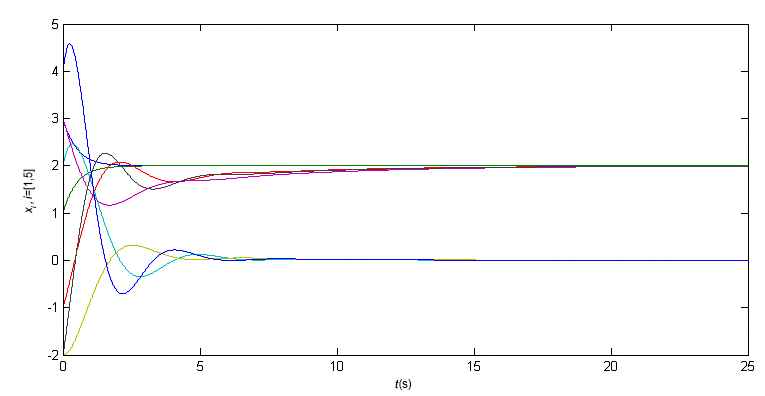
Flock guiding of five hybrid agents.
During simulation, the initial values of the agents were listed as follows
From Figure 2, the ultimate flock guiding position is 2, it is the average of the initial values of agents 1 and 2. So, in this respect, only the root block agents have their role being played in the ultimate goal of flock guiding. It is much more interesting about the second sub variables of agents 3–5, all of them were rendered to zero because of the damped factor of theirs. It seems frustrated that, the velocity signals of the agents at leaf block are not available sometimes. However, all of the second sub system states can be observed, it is a standard way to design observers for them. And in this point, this should not be an excuse to devalue our contribution here. And this is customary, because for the fixed ultimate goal position, the velocity sub variable must be ceased. Of course, the ultimate goal can be adjusted if we like, we can regulate the ultimate goal position by manipulation the coupling coefficients of root block nodes.
2.3. Some Comments
Flock guiding of hybrid agents via root block has its potential contributions at the following respects: First of all, in the easy to get and easy to use style of the contemporary network world, privacy protection problems are becoming more and more pressing, in helps of our idea here, the key information are strongly suggested to be kept in root block agents. Secondly, infrastructure cyber physical system like smart grid networks, transportation networks, can be kept immune from the injected attacks if only the small number of the key root block nodes are kept shield from the hackers. And the third, root block agents and leaf block agents have different dynamics, can conveniently be specified, paired connections of root block nodes and leaf block nodes can be tagged into block chain, which then strengthened the safety further. Pros of our suggested scheme are so obvious, and without doubt, we should continue our pursuing to this amazing topic. And some cons should be overcome in the near future, such as the injected invaders in the leaf nodes could not change the ultimate goal position indeed, but they could make the process to the ultimate goal position so difficult, via disturbing the topology of the leaf block agents connected graph. Problems like this one would be kept as our focus.
3. CONCLUSION
In conclusion, to realize the security of the flock guiding, the ultimate goal of the flock, should be exposed to only several key agents, and they can be assigned as the root node agents, as to the leaf agents, for their popularity is so massive, they should be kept from the secrets of the ultimate goal. Flock with secrets keeping is made possible here with root node and leaf node decomposition.
System complexity, which is so elusive, could not be easily explained if we are unwillingly exposed to the concrete systems. The road to clarify the complexity can be made tractable through the following exemplified engineering systems as well as the theoretical exploration. Instance like high performance vehicle driving, which was spearheaded in Jia [4] and thereafter individualized designed in Jia [5], can be the justified pilot scale systems. As to the large quantities complex systems, not only the object itself, but also the endured hostile environment, will be an impediment for the successful manipulation of them. Time varying delays, uncertain and unreliable information, annoying disturbances, and multi-inputs multi-outputs, can also be the adversary factors. Adaptive scheme was born to fix them, and this can be referred to Jia [6]. Reductionism should not be the only way to deal with the complex system, but it should be kept in mind at first, for the first step we should know the system locally in detail to grasp the whole system globally, and in this way, refined analysis and control of the complex systems are necessary. Refined control of leader follower system according their roles of the leader agent, follower agents that have connected path with the leaders, the follower agents that are failed with the connection of the other agents, and the targeting agent which represent the ultimate goal position are recommended also [7]. So, flock guiding of hybrid agents via root block, which make the ultimate goal position invariant even with some adversary leaf agents, will be much more capable candidate for the robust flocking control of agents system.
ACKNOWLEDGMENTS
This work is partially supported by NSFC Grant (61340041 and 61374079) and the Project-sponsored by SRF for ROCS, SEM to Yunzhong Song as well as Natural Science Fund of Henan Province (182300410112). The root block and leaf block flock guiding idea is benefited from the monograph, written by Lu, et al. [8].
Authors Introduction
Dr. Yunzhong Song
 He received his PhD from Zhejiang University, China in 2006. He is a Professor in the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are Multi-agent Systems and Complex Networks.
He received his PhD from Zhejiang University, China in 2006. He is a Professor in the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are Multi-agent Systems and Complex Networks.
Mr. Ziyi Fu
 He is a Professor in the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are electrical drive system and system integration, especially fault detection and diagnosis.
He is a Professor in the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are electrical drive system and system integration, especially fault detection and diagnosis.
Dr. Fuzhong Wang
 He is a Professor and also the Executive Dean of the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are power system transmission and control, process control especially fault detection and diagnosis.
He is a Professor and also the Executive Dean of the School of Electrical Engineering and Automation, Henan Polytechnic University, China. His main research interests are power system transmission and control, process control especially fault detection and diagnosis.
REFERENCES
Cite this article
TY - JOUR AU - Yunzhong Song AU - Ziyi Fu AU - Fuzhong Wang PY - 2019 DA - 2019/03/30 TI - Flock Guiding of Hybrid Agents via Root Block JO - Journal of Robotics, Networking and Artificial Life SP - 245 EP - 248 VL - 5 IS - 4 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.190220.008 DO - 10.2991/jrnal.k.190220.008 ID - Song2019 ER -
