Infection Waves in Pandemics and Risk Prediction: Physical Diffusion Theory and Data Comparisons
- DOI
- 10.2991/jracr.k.210609.001How to use a DOI?
- Keywords
- COVID-19; infection waves; community spreading; diffusion theory; data; predictions; policies
- Abstract
We predict the magnitude and estimate the uncertainties of the spread, growth and maximum expected long-term infection rates that affect emergency policies and plans. For the COVID-19 and 1918 viral pandemics, large second or successive peaks, waves or plateaux of increased infections occur long after the initial rapid onset. The key question is what physical model can explain and predict their occurrence trends and timing? We establish the principal that the timing and magnitude of such increases can be based on the well-known physics of classical diffusion theory, so is fundamentally different from the commonly used multi-parameter epidemiological methods. This physical model illuminates our understanding of the societal viral progress, providing quantitative predictions, estimates and uncertainties supporting risk decision-making and resilient medical planning. We obtain an approximate relation for predicting the risk of the observed magnitudes, timing and uncertainties of second and more waves, as needed for proactive emergency pandemic planning, bed count and decision-making purposes. The dynamic results and characteristics are compared and fitted to data using just two physical parameters for a number of countries and regions, and the concept shown to apply for both entire national and local regional populations. The present analysis quantitatively shows how much the timing and magnitude are reduced by more learning and effective countermeasures. The medical system and health policy must recognize and pro-actively plan for such inexorable diffusive spread and large residual infection waves.
- Copyright
- © 2021 The Author. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION: TYPICAL INFECTION PATTERNS AND REPEATING “WAVE” PHASES
Health crisis policy and decisions are based on infection rates so need quantitative predictions of risk trends, while medical system pandemic planning and response often depends on projected emergency bed count capacity which lag infection rates. Since viral pandemics exhibit successive waves or peaks of infections, the key question is what physical model can explain and predict the risk of their occurrence, size trends and timing? The present note expands the numerical study idea by Aciola [1] by examining if the dynamic community-wide spread can be described and understood using classical diffusion theory.
To avoid confusion, the relevant fundamental physics is completely distinct from the use of the term “diffusion” by sociologists and political scientists to qualitatively explain the varying implementation of pandemic countermeasures and policies between nations [2].
The onset and subsequent progress of pandemics such as H1N1 in 1918 and COVID-19 (aka SARS-CoV-2) in 2020, are known to be characterized by multiple increases or “waves” of infections, peaking, declining and returning over many 100’s of days. We do not re-iterate all the well-documented features of pandemics and their behavior [see, e.g. 3–6], or the many and various person-to-person infection pathways and mechanisms [see, e.g. 7,8]. We distinguish between: the dominant mechanisms of initial (direct and local transmission) rapid spreading for the first wave; and subsequent slower community spreading and transmission for producing the second and more waves (within region/country). We postulate the first peak or “wave” is the result of rapid but mainly externally introduced infections as the virus opportunistically attacks the first susceptible and unaware hosts, and increases limited according to initially rapid (few days) transmission and incubation timescales. Infections grow exponentially by unconstrained random person-to-person transmission in an initial sample population or local neighborhood without prior resistance or effective countermeasures. The initial peak (which we term here Peak 1) is reached in about 30 days until social and Non-pharmaceutical Intervention (NPI) countermeasures (e.g. improved hygiene, social distancing, improvised quarantines, public awareness, etc…) effectively counterbalance the growth in the infection rate. The Peak 1 wave subsequently declines universally according to learning theory from adopting such simple countermeasures [9,10].
However, zero risk or rates are not achieved or achievable (as known for perennial influenza) due to hidden residual infections, asymptomatic cases, and/or undetected importations or “clusters”, which ensure the virus continues to be slowly, inexorably and randomly distributed. The virus progressively becomes distributed throughout the community, and largely undetected or hidden progressively continues to spread. This initially low level of mainly internally introduced or enabled community-wide spread inside countries is widely observed, even in island states where complete entry and viral import restrictions, mandates or controls are possible (like Hawaii, Australia and New Zealand). Since the initial infective decline is competing against diffusive increase, the second wave onset only starts to be discernable or noticeable many weeks after the Peak 1. Eventually, after about 100 days, a second distinct “wave” or increase toward a plateau (which we term here Peak 2) is more clearly observed, which is also reached before some balance is achieved between increased diffusive transmission and effective countermeasures.
While not exactly followed by all regions, these overall data patterns, trends and surges are compelling and apparently independent of continent, culture, society or century, as shown in Figure 1 (the rates per day are normalized to the first peak and the temporal evolution measured in days exceeding 100 initial infections as a nominal start or pandemic threshold). We hypothesize that the second and subsequent waves have a fundamentally different physical spreading character, having moved from the early rapid infection phase of initial local populations dominated by rapid personal incubation timescales (3–5 days) and contacts to slower and more extensive overall community spreading (50–100 days) dominated by slower societal interactions, more cautious behaviors and residual infections.1 These phases may of course overlap or not be entirely distinct everywhere, so we look to data for guidance, quantification and verification.

General idealized trends of pandemic infection waves over the last century, with daily infection numbers normalized to the first peak. (1) Initial random infections, n0, from external introduction with rapid rise (incubation limited timescale, G). (2) Exponential rise to first wave peak, nM1, in circa 20–30 days, dM1. (3) Decline due to learning (countermeasure like awareness, hygiene, and social distancing…), k. (4) Minimum achievable infection rate (or detection threshold), nm. (5) Second “wave” apparent onset, n02, at circa 50–100 days (community spread limited timescale). (6) Second rise, n(d), from random inter-community spread (societally embedded). (7) Second peak or plateau, nM2, at about, dM2, circa 100+ days often larger than first peak. (8) Plateau or decline due to learning, countermeasures plus human host spreading limits. (9) Minimum “acceptable” or achievable rate achieved again. (10) Additional waves possible (annual, seasonal, social…).
The usual Susceptibility-Exposed-Infected-Recovery (SEIR) and R0 models for the infection rate [11–13] have been fitted using some seven parameters to first peak rise and decline data [e.g. 14,15] where the infection increase rate is limited by personal incubation timescales. Previous work on second waves [16] solved the standard SEIR model plus a further two equations, giving six first-order differential equations with eight variable parameters, four representing various assumed socio-economic countermeasures (e.g. “lockdown”, school closure, perception and learning). Despite the SEIR approach being known to be inaccurate and not predictive [13], three parameters were first fitted or “calibrated” to data, while varying the five remaining of the eight parameters gave differing Peak 2 to Peak 1 ratios. The results showed oscillations, with Peak 2 at 240 days and then a decline, and that “In some cases, the second peak was higher than the first peak, while for other parameter combinations it was lower.” It was concluded “a second wave of COVID-19 on account of the coupled behavior-disease feedbacks… will characterize many populations” [16]. There were no comparisons given to actual data as in our new approach.
To model the societal medico-physics, and avoid so many empirical parameters, we postulate that after the initial peak this subsequent community-wide spreading is dominated and governed by random diffusion, with infections seeping steadily, systematically and inevitably throughout the population, and largely independent of countermeasures. As first pointed out by Aciola [1] for the first peak using purely numerical solutions: “a simple diffusion model treats each individual in a population as a Brownian particle …added to this model is the incubation period of the virus and a probability of transmission of the virus if individuals are closer than a certain distance.” This fundamental idea reflects the reality that individual infection transfers and opportunities are statistically random; and of not being able to identify, track, eliminate or monitor all the encounters and social interactions of every infected person and prevent such transfers. For a whole society, we are not looking at individuals but entire populations and overall societal behaviors and the resulting infection trends.
Therefore, for second or other successive waves the problem and equation to be solved is essentially Fick’s or Fourier’s Law, a second order differential equation, where the net rate of change of infections at any location is proportional to the incremental infection gradient. For any infection number, n, at any time, t, conventionally, without additional internal or imported infection sources:2
The community-wide diffusion coefficient or diffusivity, D, physically represents all random person-to-person and intra-societal cross infections and is the key parameter to be deduced from observational data. Importantly, Equation (1) is a second order differential equation, so: (a) is fundamentally more general than the first order differential equations used in classic R0 and SEIR epidemiological spread models with multiple adjustable parameters; (b) contains a very limited number of variable but physically-based coefficients that can be directly tested against or fitted to data; and (c) therefore able to draw on the foundations and prior knowledge of classical physics and methods for heat and concentration diffusion. To illuminate the physics, we seek an analytical solution to Equation (1) that is testable against publically available data for the second and/or subsequent waves.
2. MATERIALS AND METHODS
2.1. Basic Theory and Postulates
Exact solutions of Equation (1) are numerical [1] whereas we only seek a working correlation to aid our understanding and enable rapid estimates for risk decision-making. For the second and successive “waves”, we make simplifying assumptions and reasonable approximations to derive a basic analytical solution form for the dynamic infection trends and the limiting physical societal transmission mechanism, the accuracy and applicability of which can be determined by comparisons to data. Hence, even if and as countermeasures are deployed, without complete isolation or elimination the virus spreads:
- (a)
by diffusion in any local region(s) or cities, becoming inevitably embedded in the wider community (regions of higher infection numbers naturally infect regions with lower);
- (b)
throughout any national or regional location, all the population is equally able to be randomly infected so the distribution of the virus is to first order homogenous and any and all infections are equally possible;
- (c)
with fundamental physics limiting the extent the rate of subsequent community spreading is described by the classic Fick’s Law with diffusivity parameters averaged over the population/region/society; and,
- (d)
being equally possible so affording a simple homogenous and one-dimensional approximation, with the number of infections, n, some fraction of the total possible, N, where usually n <<< N, depending on the overall community transmission mechanisms, societal behaviors, and countermeasure effectiveness.
For some overall societal characteristic effective transmission scale, L, after an elapsed time measured in days, d, the rate of change of infections or number counted on any day, n(d, L), in one dimension Equation (1) becomes,
Using the usual non-dimensional formulation,
Prior physics and classic texts provides the analogous Fourier flux solution satisfying Equation (3) [1,17,18] and is the usual error function,
2.2. Approximate Correlation Derivation for Wave Timing and Magnitude
To guide our thinking for present correlation and risk trending purposes, for the large-scale ratios, L/(4Dd)1/2, relevant to whole communities and regions during diffusion, we can retain just the first term in the series expansion of Equation (4) [see 18 #586], so:
Usually, the minimum rate number, nm << n(d) and n02, so
Using Equations (5) and (6) for describing the second wave requires determining just two adjustable but physically based parameters: the diffusion coefficient, D (m2/day), and the assumed characteristic or effective length scale, L (m), assuming the Peak 1 parameters (G and k) still prevail. Both of course depend on some integration/aggregation of all the exact overall societal viral transmission mechanisms (person-to-person, aerosols, crowds, contamination, random exposure…), which we simply assume to exist.
We can then also estimate the relative size and timing, dM2, for attaining Peak 2 when the diffusive growth is eventually balanced, assuming the same NPI learning countermeasures are used (e.g. social distancing, improved hygiene, public awareness etc...). For Peak 1, the decrease in the increasing rate decreases when the daily transmission and incubation increase number, nM1, is comparable to or balanced by countermeasures and public awareness. For some learning constant, k, representing the overall countermeasures effectiveness and resilience during and after Peak 1 [10],
Here, the parameters for incubation growth for any initial viral variant, G, learning recovery, k, and peak day, dM1, are known from the Peak 1 prior data trends (Figure 1), and allows quantification of countermeasures by evaluating, k. This second wave or “curve flattening” semi-plateau has an asymptote given by
Given this approximate second plateau, from Equation (8) the predicted Peak 2 to Peak 1 rate size ratio is of order,
3. RESULTS
3.1. Comparisons of Theory to Pandemic Second Wave Onset Data Trends
Excellent data for daily infection numbers are available in downloadable spreadsheet format [19] from January 2020, and from WHO, Johns Hopkins University and other reliable sources, including local state data from Departments of Public Health websites. As a reference origin, we adopt the initial detection/reportable threshold of n > 100 total cases as a datum for the definite onset of significant infections, d = 0, and varying this threshold has only a minor impact as Peak 1 usually occurs within 20–30 days.
The origin of the minimum at the second wave onset, θ(d02), is the lowest daily infection count continuously achieved following the exponential decline from Peak 1, and used to normalize all subsequently increasing infection rates, R* = θ(d)/θ(d02). To encompass widely separated and differing societies, we performed test calculations for ongoing and continuing infection data showing distinct second waves as listed in Table 1 for UK, Italy, France, Canada, and Australia (as of October 15, 2020). The latter is specifically chosen as being a distinct “island state” with comparatively low (but non-zero) rates but second waves (or “clusters”) despite extensive internal controls and border/entry restrictions.
| Country/region | Start d = 0, 2020 | Peak 1 rate | θ(d0)day | D (m2/day) | L (m) |
|---|---|---|---|---|---|
| Australia | 18 March | 715 | 81 | 0.013 | 10 |
| Canada | 12 March | 2760 | 53 | 0.012 | 7 |
| France | 5 March | 4610 | 107 | 0.014 | 10 |
| Italy | 25 February | 6560 | 100 | 0.014 | 12 |
| UK | 7 March | 5290 | 120 | 0.014 | 9 |
Country data with first peak and distinct second wave
Comparisons to the theory are shown in Figure 2, where the fits were derived using the range of 0.012 < D < 0.014 m2/s and 7 < L < 12 m-values as shown in Table 1 and are largely independent of country or societal culture. These fitted parameter values in Table 1 indeed are consistent with a whole society reaching a peak or plateau at
Second wave trends compared to theory.
The overall agreements with such disparate data are not perfect (Canada and UK exhibit over predictions) but the salient overall slow growing trend and 100–200 days timescales are reasonable (especially for Australia, France and Italy) given the approximations in the theory. Capturing the steep exponential onset is also inexact at present. The Australia case with literally different boundary conditions on infection control shows clearly that Peak 2 can also be reached, while terminating the second wave growth as also observed in the classic 1918 pandemic [4,20,21].
3.2. Estimating Second Wave Magnitude and Uncertainties
When recovery from Peak 1 is not always complete, n02 > n01, ensuring that Peak 2 daily rate is larger and what is actually observed, affecting emergency pandemic planning and decision-making. For countries already known to exhibit second wave peaks with recovery/decline, Australia actually had a Peak 1 to Peak 2 infection rate magnitude ratio,
| US state | Peak 1 rate, nM1 | Peak 2 rate, nM2 | Ratio, R* |
|---|---|---|---|
| Alabama | 346 | 2143 | 6.2 |
| Arkansas | 323 | 992 | 3.1 |
| Colorado | 526 | 1139 | 2.2 |
| Florida | 1269 | 13965 | 11 |
| Georgia | 1333 | 4813 | 3.6 |
| Idaho | 131 | 878 | 6.7 |
| Kansas | 345 | 1040 | 3 |
| Louisiana | 1857 | 3840 | 2.1 |
| Nebraska | 645 | 1286 | 2 |
| Washington | 584 | 959 | 1.6 |
US state data with first peak and distinct second wave
Following these predictions and estimates, we examined the apparently unique case of China3 as: (a) being the original source of the pandemic reaching Peak 1 in 26 days of 4000 cases per day by February 13, 2020; (b) exhibiting a rapid decline from Peak 1 which followed learning theory and presaged global recovery trends [9]; (c) thereafter reporting low daily infection rates (claimed to be mainly importations), with a barely discernable second wave Peak 2 reported as 276 cases per day on July 31; and (d) maintaining almost complete control of population movement and mobility, with enforced NPI mandates and personal contact tracking. With low and fluctuating numbers, it is difficult to uniquely pinpoint the second wave onset day, dn02, and rate value, n02, taken here as nominally day d = 100 with just two reported cases per day, suggesting n02/n01 ~ 2/100 = 0.02, which would give nM2/nM1 ~ 0.16, compared to that reported or observed of 276/4000 ~ 0.07.
The comparison of the data to the fitted theory [Equation (5)] is shown in Figure 3 using the same D = 0.012 m2/day and L = 10 m values found for the Table 1 countries. This similarity suggests the fundamental physical diffusion and societal transmission processes are globally the same; and that China exhibits the same long-term embedding in the community as everywhere else. In addition since the Peak 1 initial recovery in China is similar to Italy and others [10], the second peak should be
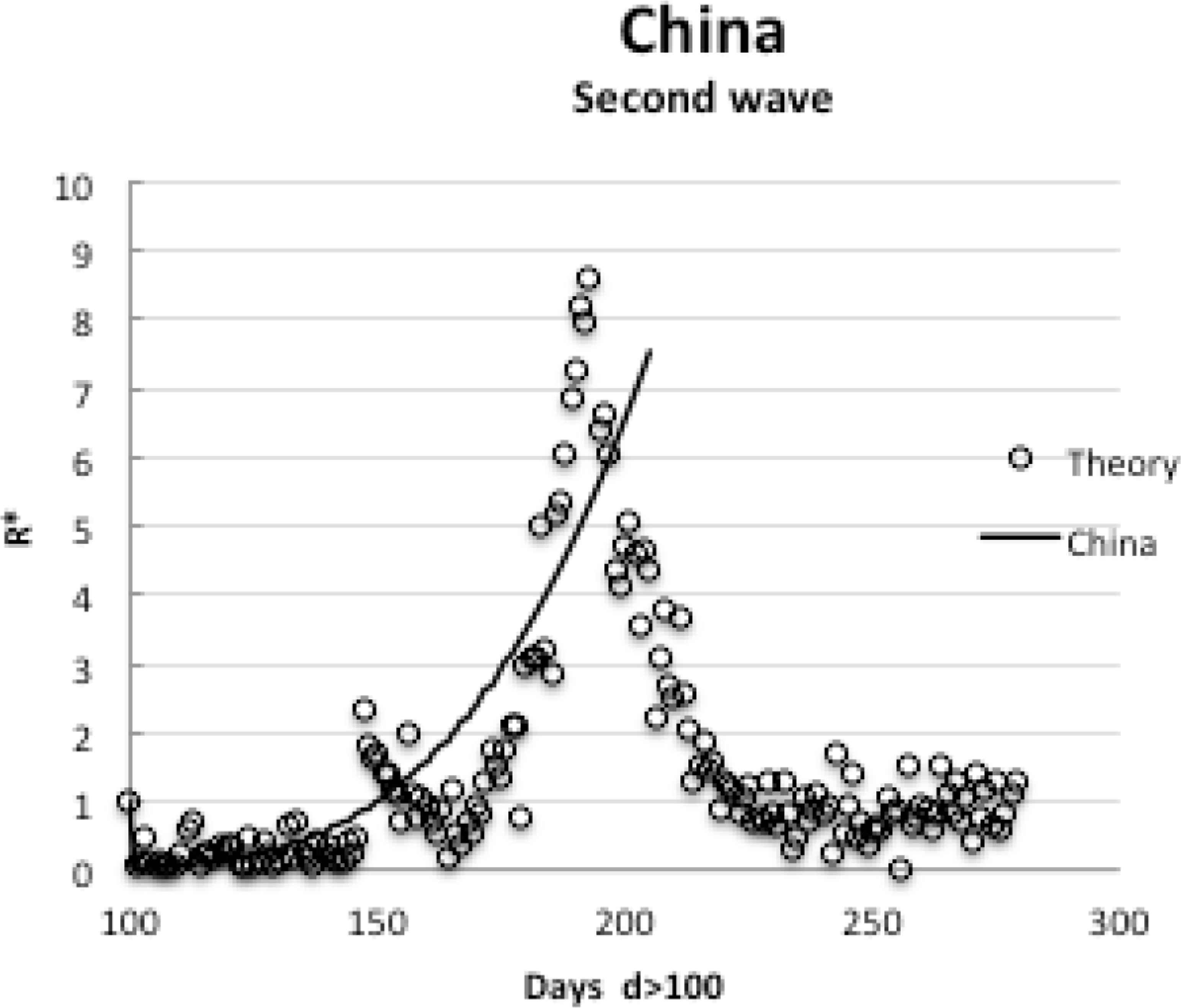
Comparison of theory to second wave data in China.
As further confirmation, currently, a wide range of second defined waves or plateaux after Peak 1 are on-going and have not yet declined [22]. Current ratio examples include: Austria (8), Belgium (9), Canada (2), Denmark (4), France (11), Germany (4), Indonesia (4), Iran (4), Israel (5), Italy (6), Nepal (9), Spain (3), Sweden (3), and UK (6). These overall ratios cover a similar range (2–12) to the US internal/regional state ratios in Table 2, and encompass the predicted estimate,
3.3. Local and Regional Peak Ratio Trends and Predictions
Insignificant initial infections may occur locally outside the initial peak regions (e.g. large cities like New York or Wuhan) but increase only after about 100–150 days solely due to slow progressive internal diffusive spread throughout the region, notably seen for US states like Alabama, Alaska, Wisconsin and some European countries. Being important for local public health risk planning purposes, we examined if an even small regional population internal to the country followed the same trends. Data were obtained directly from the state-run East Idaho Public Health District (EIPHD) covering Bonneville County, Idaho (where the author lives), with a local population only circa 120,000, a rural and urban setting without a first local first peak despite Idaho overall having a Peak 1 from infections cases occurring in other locations (Figure 1). The second wave arrived and emerged after about 100 days after the first onset, a similar timeframe to the second wave onset for the whole state data in Figure 2.
Figure 4 compares the data to Equation (8), with the starting, d = 100 days after first exceeding 100 initial cases in the whole state (Figure 1). The “best” theory fit shown uses the same values for D (0.012 m2/day) and L (10 m) as for China and all the large countries in Table 1 and encompasses the data. This is a major and quite unexpected confirmation that the diffusion concept represents infection risk growth throughout whole and totally disparate societies with large differences in population and enforced or “mandated” countermeasures.
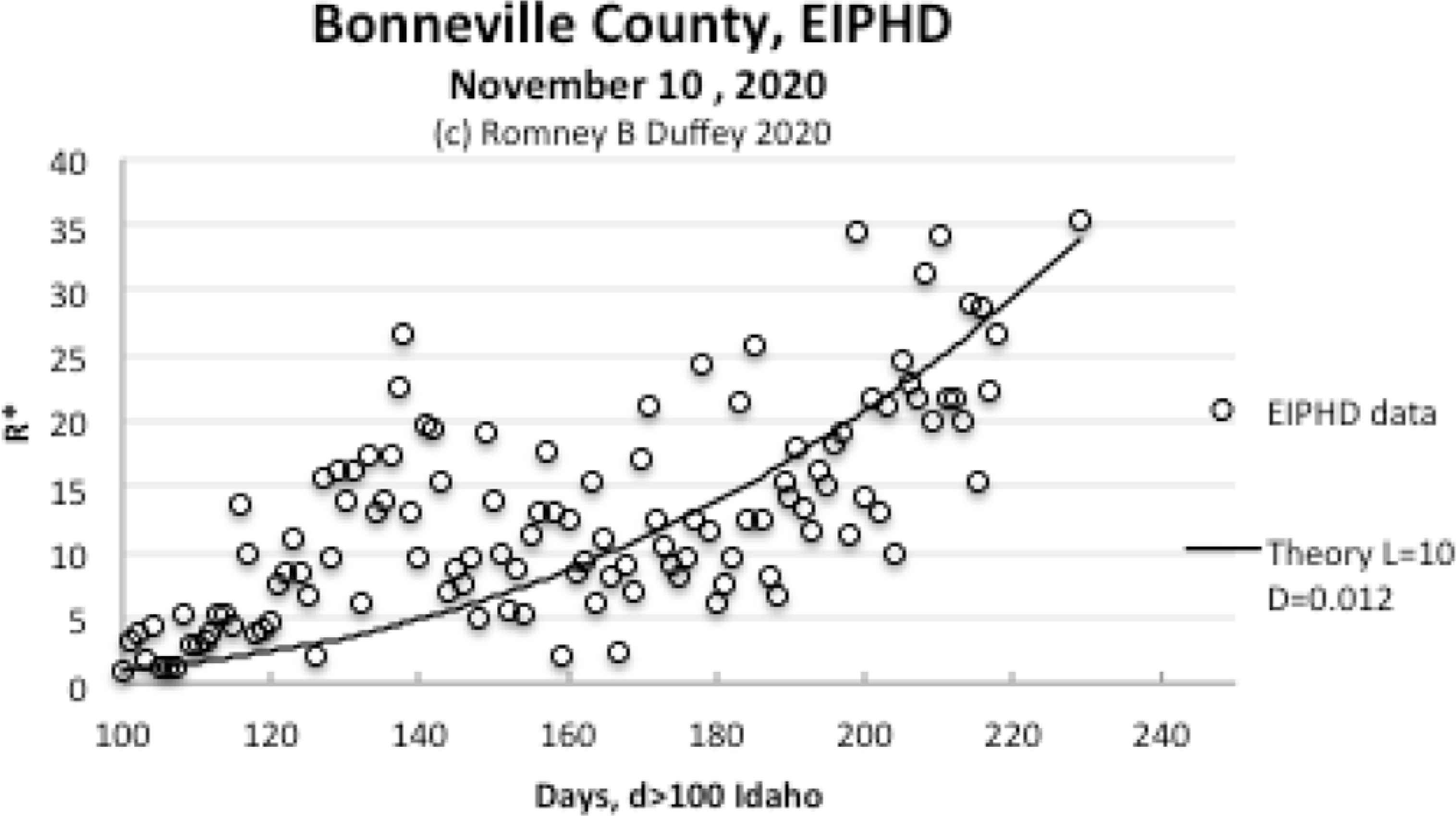
Internal second wave onset in local region of a USA state.
In passing, note that despite continued controls and countermeasures, New York State is currently exhibiting the symptoms of the onset of a second wave after day 150 (August 7, 2020), with cases slowly and inexorably rising. This is a pure prediction for a possible second wave of similar magnitude to Italy.4
For successive (third or more) waves arising in the ever-widening infected community, the assumption is each wave is superimposed on (or builds upon) any base or remnants of predecessor infections from the earlier wave(s). In USA and Japan, despite being totally distinct and distanced societies, distinct Peak 3 occurred after a further 100 days after Peak 2, so an initial scoping analysis was performed using the identical L and D values derived for Peak 2 to predict the USA Peak 3 growth, as shown in Figure 5.
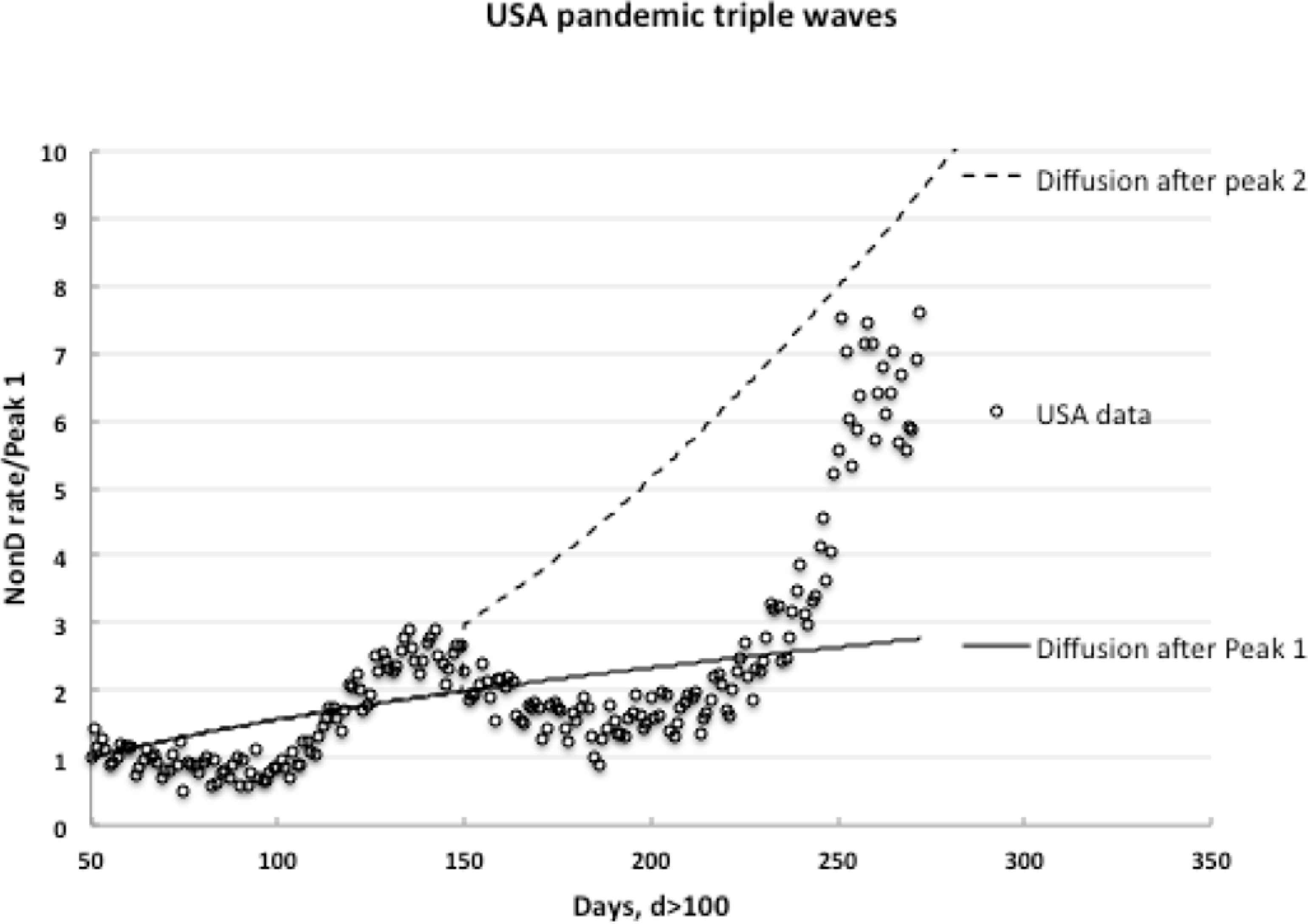
Initial scoping third wave predictions for the entire USA (data for March 4 to November 10, 2020).
Although a simplified and pessimistic over-prediction, the overall trends are reclaimed, with the ratio,
4. DISCUSSION: THE RISK AND UNCERTAINTY OF LARGE SUCCESSIVE WAVES AND VACCINE EFFECTIVENESS
We need to pro-actively plan, but as far we know there have been no other second wave size and timing predictions with diffusion adopted as the dominant limiting physics for community spreading. Predicting second wave timing and magnitude is a difficult task with considerable uncertainty so we have tried to find a simple solution to this hard problem while not claiming complete accuracy. Despite significant variability and uncertainty, after a few 100 days second waves (up to a factor of 10 larger than Peak 1) are to be expected, and this elevated risk should be pro-actively planned and managed.
Given diffusion represents the limiting societal transmission phenomena, the present simple one-dimensional theory cannot replicate every detail for more complex scenarios but can plausibly explain as follows:
- (a)
no discernable first peak appears because multiple numerous initially rapid infections dominate initial national counts, followed by more widespread cases over the 100’s of days of slow diffusive timescale, notably as observed in Argentina and Brazil as well as in local regions.
- (b)
only a slow recovery occurred after the initial rapid Peak 1, so many thousands of cases were still occurring during the diffusion masking the second wave onset which is then superimposed after about 150 days, as notably demonstrated by Russia and the USA.
While beyond the scope of the present paper, these detailed trends really require more complex intra-regional analysis. The limiting overall societal viral transmission mechanism being diffusion via widespread societal contamination and viral presence replaces the usual paradigm of traditional SEIR and C0 epidemiological models which assume the new infection rate is directly proportional to the number originally infected [e.g. 11–13,16].
Ascribing physical significance, the observed characteristic diffusive length scale of approximately 10 m is an effective overall societal transmission distance not inconsistent with feasible transmission dimensions [21]; and not coincidentally is a typical room, home or store dimension where people and societies interact. The order of magnitude for the coefficient, D, is a factor of more than 10,000 smaller than the 10−2 to 10−3 m2/s associated or expected for local airborne atmospheric particulate or direct aerosol spreading mechanisms [see, e.g. 23,24] reflecting the slow onset of second and other waves are simply the consequences of normal human and personal interactions and overall societal risk-taking behavior [25], as exemplified in the USA by the contrasting weak and strong policies adopted in Florida and California, respectively.
As to the important question of quantifying effectiveness of vaccines as a pharmaceutical intervention or countermeasure, in principle our learning model [9,10] allows direct estimation of the revised, k, value in Equation (7) describing the exponential decline from Peak 3, an exercise that is on-going. The new predictions and comparisons illuminate public health policy and risk planning. The present analysis quantitatively shows timing and learning and adopting effective countermeasures reduce magnitudes but cannot eliminate infections completely. Since pandemic second and more waves persist, the only perfect diffusion “barrier” or so-called “circuit breaker” is indefinite isolation for everyone everywhere, which is neither feasible nor desirable.
5. CONCLUSION: BEING PRO-ACTIVE IN RISK PREDICTIONS
We have established the principal that the timing and magnitude of long-term infection increases or successive waves can be based on the well-known physics of classical diffusion theory. This simple concept explains and predicts the successive “waves” or recurrences of higher infection numbers 100’s of days after the first peak in case rates, with the subsequent inexorable dynamic community-wide spread and embedding of infections. If the pandemic started in localized centers, this diffusion process represents the inevitable but “imperfect” subsequent transmission of viral infections independent of strain due to prevalent, pervasive and persistent societal behaviors, and is a physical model fundamentally different from the proportional rate assumptions of traditional SEIR and C0 epidemiological models.
To enable original trend, size and timing predictions and obtain physical insight, we have derived explicit approximate equations for dynamic infection numbers using the simplest homogenous one-dimensional diffusion model. Two physically-based variables, a characteristic societal length scale and an effective community wide diffusion coefficient, have been fitted to the infection rate data for a wide range of countries and local regions of differing societal behaviors and countermeasures, showing that the effective diffusivity and characteristic scale are universal. The timing and relative size of the second and subsequent larger peaks or semi-plateau is also limited by the relative (in)effectiveness of NPI countermeasures and societal learning effects. Medical system planning and emergency bed count capacity projections encompass peak wave magnitude ratios, R*, of up to about 10 times the initial peak infection rate after about 100 days. We know of no other estimation method or published number for the risk of second and subsequent peaks and for estimating uncertainties. The policy and risk planning implications of such inexorable diffusive spread must be by recognizing potentially larger infection waves will inevitably occur and pro-actively planning for that eventuality.
CONFLICTS OF INTEREST
The author declares no conflicts of interest.
ACKNOWLEDGMENTS
The author is indebted to all the contributors to infection data collection and reporting that have made this work possible, and Ms. Geri Rackow for supplying the EIPHD data files. He also thanks Dr. E.D. Hughes for his important critique and suggestions; and Professors Enrico ZIo and Francesco D’Auria for their comments, encouragement and extended dialogs on this topic.
NOMENCLATURE
- D
– Effective community diffusion coefficient;
- d
– Elapsed time in days;
- G
– Initial characteristic infection rate;
- k
– Learning countermeasure characteristic rate;
- L
– Characteristic transmission societal scale;
- L*
– Diffusive scale ratio, (4Dd/L2)1/2;
- NPI
– Non-pharmaceutical intervention;
- n
– Number of infections in any day;
- R*
– Infection number ratio, R* = θ(d)/θ(d0);
- t
–Time;
- θ
– Non-dimensional number ratio; [Equation (5)].
- M1
– Maximum value at Peak 1;
- M2
– Maximum or asymptotic value of second wave;
- m
– Minimum achieved or attainable value;
- 0
– Initial or beginning value;
- 01
– Initial value for onset of Peak 1;
- 02
– Initial value for onset of second wave.
Footnotes
We utilize infection rates as a leading indicator of spread, while public health officials usually focus on death numbers and rates which lag infections; and which fraction of infections is variable being highly dependent on the propensity, vulnerability, medical treatment and ages of the population so cannot be solely diffusivity dominated.
For a source add to the RHS a term, say ns′, being the number per unit time.
This case study was suggested by Professor Francesco D’Auria as being of particular importance in terms of the total population at risk.
Note added in March 2020: As predicted in October, such a second wave in fact occurred in Italy with Peak 2 in mid-November with rate magnitude ratio nM2/nM1 ~ 8.
REFERENCES
Cite this article
TY - JOUR AU - Romney B. Duffey PY - 2021 DA - 2021/06/16 TI - Infection Waves in Pandemics and Risk Prediction: Physical Diffusion Theory and Data Comparisons JO - Journal of Risk Analysis and Crisis Response SP - 67 EP - 74 VL - 11 IS - 2 SN - 2210-8505 UR - https://doi.org/10.2991/jracr.k.210609.001 DO - 10.2991/jracr.k.210609.001 ID - Duffey2021 ER -
