1. Introduction

Many researchers have focused attention on designing force control schemes for robot manipulators in the past decades. As an end-effector of robot manipulators interacts with an environment, the existing contact force must be regulated to protect the end-effector and environment against serious damages. To solve this problem, the hybrid position/force control approaches [1–2] have been proposed to guarantee a smooth transition from position control to force control. However, the formulation of hybrid position/force control cannot be easily achieved. Also, many of these control schemes require the exact kinematics and dynamics of robotic system; hence, an adaptive Jacobian position/force control [3] has been developed which does not require all the knowledge of the robot manipulator.

In order to provide a unified solution of the position and force control, the impedance control schemes [4–6] have been developed for robot manipulators. An impedance model is designed to describe the dynamic behavior of a robotic system when interacting with the environment. It is worth noting that impedance control methods are strongly affected by the uncertainty associated with the nonlinear dynamics of highly coupled robotic systems, unknown environments and external disturbances [7]. Therefore, the performance of control system is dependent on how well the uncertainty can be compensated [8]. Adaptive impedance controllers [9], robust impedance controller [10], learning impedance control [11] and force tracking impedance control [12] have been developed to tackle uncertainty. It should be emphasized that the majority of impedance controllers are based on torque control strategy such that the proposed control laws require the dynamics of robot manipulator and also the role of robot's motors is excluded from the control problem.

To consider the whole robotic system including robot manipulator and motors, a regressor-based variable-structure controller [13], the min-max scheme [14] and a generalized impedance controller [15] have been proposed. By using the voltage control strategy [16–17], the impedance control of electrically driven robots has been proposed [18]. The main idea behind the voltage control strategy comes from the fact that the manipulator dynamics can be taken into account indirectly as measuring the motor currents.

An adaptive impedance control of human-robot cooperation [19] has been developed. In this control method, linear quadratic regulation has been formulated to minimize tracking errors and to obtain an optimal impedance mode of human. An adaptive neural impedance controller [20] for robot manipulators has been proposed by considering uncertainty and input saturation. An adaptive control method [21] has been designed for tracking purpose of uncertain robotics in order to compensate parametric uncertainties, unmodelled dynamics and external force disturbances without a priori knowledge about upper bound of uncertainty. An adaptive fuzzy neural network force approach [22], robust neural network [23] and robust adaptive neuro-fuzzy controller [24] for hybrid position/force control of robot manipulators have been developed, which interacts with unknown environment. A PID-fuzzy controller was developed to deal with the nonlinear contact force control problem [25].

This paper presents a voltage-based model-reference impedance control approach using a fuzzy uncertainty estimator for the electrically driven robot manipulators. In the proposed control scheme, a desired impedance is used as a model-reference in such a way that this model-reference could provide a reference signal for a robot in both tracking and contact situations. As the interaction between an end-effector and an environment occurs, the contact force is exerted to the model-reference and the robotic system receives the output of model-reference as a desired trajectory and thus the aim of the controller is to reduce the difference between the task-space desired trajectory and the desired impedance model. In order to tackle difficulties in the analysis of the motion equation in task-space, a specific transformation is used and a pertinent controller is designed in the joint-space. Furthermore, two control terms namely, a robustifying term and a fuzzy uncertainty estimator are employed in the proposed controller: (i) to improve the performance of control system; (ii) to compensate un-modelled dynamics and external disturbances.

In the remainder of this paper, the robotic problem formulation is discussed in Section 2. In section 3, fuzzy uncertainty estimation is introduced. Section 4 develops the impedance design. The proposed robust control approach and the stability analysis of the control system are developed in section 5. Section 6 illustrates the corresponding simulations to validate the theoretical results. Finally, Section 7 concludes the paper.

2. Problem Formulation

The dynamics of a robotic system which is in contact with a frictionless rigid environment consist of n links interconnected at n joints into an open kinematic chain of rigid links and the geared permanent magnet dc motors are described as [26]

where q ∈ Rⁿ denotes the joint coordinates and is the vector of joint positions, D(q) ∈ R^n×n is the inertia matrix, C(q,q˙)q˙∈Rn the vector of centrifugal and Coriolis torques, G(q) ∈ Rⁿ the vector of gravitational torques, F_e ∈ R^m the contact forces vector, τ_r ∈ Rⁿ the input torque vector of robot manipulator. J_m, B_m and r are the n × n diagonal matrices for motor coefficients namely the actuator inertia, damping, and reduction gear, respectively. K_m ∈ R^n×n is a diagonal matrix of the torque constants, I_a ∈ Rⁿ is the vector of motor currents, v ∈ Rⁿ is the vector of motor voltages and φ(t) ∈ Rⁿ is a vector of external disturbances. R, L and K_b represent the n × n diagonal matrices for the coefficients of armature resistance, inductance, and back-emf constant respectively. J(q) ∈ R^m×n is the Jacobian matrix of the robot arms, which converts the joint space to the task space as where x ∈ R^m is the vector which determines the position of the end-effector. The time derivative of equation (4) can be written as

We consider that m = n and the robot trajectory is never in a singular configuration, i.e., the inverse of the Jacobian matrix always exists. Note that vectors and matrices are represented in bold form for clarity. By considering (1)–(3), one can present the state-space model as

where v is considered as the inputs, z is the state vector and f(z) is of the form in which,

A highly coupled nonlinear system in a non-companion form is shown by the aforementioned state-space equation.

3. Fuzzy Uncertainty Estimation

One can represent the voltage equation (3) as

in which μ(t) denotes the uncertainty in form of where LI˙a and φ(t) are expressed as un-modeled dynamics and external disturbances respectively. By considering (9), uncertainty can be represented in scalar form as

In order to estimate μ_i, the fuzzy estimator is employed. The motor current I_ia and the joint velocity q˙i and v_i(t–ε) are considered as inputs of fuzzy system. To estimate the uncertainty, v_i(t) is not available. Instead, v_i(t–ε), which is the past information of v_i(t), is given as the input of the fuzzy system, where ε is the time delay. By allocating three membership functions named as Positive (P), Zero (Z) and Negative (N) to each fuzzy input, 27 fuzzy rules will cover the whole space. The linguistic rules of fuzzy are utilized in the Mamdani type as

where Rule l represents the l-th fuzzy rule for l = 1, … ,27, fuzzy membership functions A_l, B_l, C_l and D_l belong to the fuzzy variables I_ia, q˙i , v_i(t–ε) and μ^i , respectively. The membership functions for input I_ia are given as follows

The membership functions for inputs q˙i and v_i(t − ε) are chosen as the same of I_ia. Also, 27 symmetric Gaussian membership functions are defined for the output μ^i in the form of

where ψ^il is the center of fuzzy membership function D_l. In this paper, ψ^il is adjusted by an adaptive law derived by the stability analysis. Using the product inference engine, singleton fuzzifier, center average defuzzifier and Gaussian membership functions [27], we select the fuzzy system for μ^i as follows

One can easily denote (17) of the form

in which Y_im = [Y_im1, …, Y_im27] is a positive regressive vector defined as

And ψ^i is an adaptive gain vector of the form

4. Impedance Design

The contact forces vector, F_e, can be presented as

where M_e ∈ R^m×m, B_e ∈ R^m×m and K_e ∈ R^m×m are represented the inertia, damping and stiffness of the environment involved in contact and x_e ∈ R^m is the environment equilibrium position in the absence of the contact force. One can take the Laplace transform from both sides of equation (21) to yield in which Z_e(s) is defined as

In contact with the environment, which is a primary goal for impedance control of robotic system, a desired dynamical behavior is defined in Laplace form as

where x_d is the desired trajectory in task-space, x_m is the output of reference model and Z_R(s) is a desired impedance given as follows where M_R, B_R and K_R represent the diagonal n × n inertia, damping and stiffness of the reference model matrices, respectively. Using (25), equation (24) can be rewritten in scalar form as

5. Robust Control Design and Stability Analysis

In section 5, our control objective is to propose an impedance model-reference controller to reduce the difference between the task-space desired trajectory and the desired impedance model. The proposed controller is equipped with fuzzy estimator in order to be robust against the uncertainty including un-modelled dynamics and external disturbances as well as a robustifying term to improve the performance of controller. The block diagram of control system is shown in Fig.1.

Fig. 1.

The Block diagram of the control system

The dynamic equation of electrically driven robot manipulators in task-space can be obtained by substituting equation (1) to (2) and using equations (4), and (5) and (9) as follows

where D_x, C_x and G_x are given as

Some properties of the dynamic equation of electrically driven robot manipulators (Eq. 27) can be expressed as follows [26]:

Let us define the error dynamics as

in which k₁ is the n × n constant positive definite matrix and e is the reference error which is the difference between the output of the closed loop system and the reference model output expressed by

Consider a following positive definite function as

Taking the time derivative of V gives that

Using (33) and (34), equation (36) yields

One can rewrite equation (27) as

Substituting (39) into (38) we have

Considering (33) and (34), one can obtain

Thus, substituting (41) into (40) yields to

In other words,

Let us define the modified velocity and acceleration in task-space as follows

By using the skew-symmetric property (31) and equations (44) and (45), one can modify (43) as

Considering linear parameterization property (32), we can write

It is noted that Yx(x,x˙,x˙r,x¨r)∈Rn×np and P_r ∈ R^n_p×1 are regression matrix and vector of parameters, respectively, where n_p is the number of parameters. By substituting (47) into (46),

By applying (49) and (50) to equation (47) and using (28–30), it can be obtained

Using (51) and also transforming the error dynamics (33) into joint space, i.e. Ξ=J(q˙−q˙r) , equation (48) can be modified as

This paper proposes the control law as

in which k₂ ∈ R^n×n is a diagonal positive definite matrix and v₁ is a robustifying term. By applying the control law (53) to (52), we have

Assume that Rkm−1r and F_e are bounded as follows

Using the Cauchy–Schwartz inequality, we have

where η ≜ η₁η₂. By considering (57), equation (54) can be written as

The robustifying term is selected as

By substituting (59) in (58) and some manipulations, we have

Assume that the uncertainty (10) can be modelled as

where ε_f is a modelling error. One can employ (18) and (61) to (60) obtaining

If the adaptation laws are chosen as

Then equation (62) is expressed as

The following assumptions are made to complete the stability analysis [26,30]:

The error dynamics, Ξ=J(q˙−q˙r) , reduces if V˙<0 . Hence, satisfying V˙<0 for equation (66) yields

Since k₂ is a positive definite matrix, then the right-hand side of (67) is bounded as

where λ_min(k₂) and λ_max(k₂) are the minimum and the maximum eigenvalues of k₂, respectively.

Using the Cauchy–Schwartz inequality and considering the upper bound of modelling error as ‖ε_f‖ < ρ, the left-hand side of (67) can be obtained

Therefore, by considering (68) and (69) in order to satisfy V˙<0

In other words

Let us define two diagonal positive definite matrices k₂₁ and k₂₂ such that k₂ = k₂₁ + k₂₂ (i.e. λ_min(k₂) = λ_min(k₂₁) + λ_min(k₂₂)), in order to satisfy

As a result, in order to satisfy (67), it is sufficient that

where β₁ and β₂ are positive constants. It is noted that V˙<0 as long as β<‖J(q˙−q˙r)‖ in which β = max (β₁, β₂). This implies that the reference error e and its time derivative e˙ become smaller out of the ball with the radius of β. As a result, the reference error and its time derivative are bounded and ultimately enters into the ball with the radius of β.

Considering assumption 2 and 3 and the proof given by [31], v, I_a, I˙a and q˙ are bounded. Since the desired impedance matrices M_R, B_R and K_R are chosen in such a way as the roots of M_Rs^{2 +} B_Rs + K_R be in the left-hand side of the s-plane and thus according to assumption 1, equations (56) and (26), x_m and x˙m are bounded. Since e, e˙ , x_m and x˙m are bounded, the boundedness of x, x˙ , x_r, x˙r and x¨r is proven. As a result, the regression matrix Yx(x,x˙,x˙r, x¨r) and Y(q,q˙,q˙r,q¨r) are bounded and following that P^ is bounded by considering (63). The boundedness of equation (19), e and e˙ result in the boundedness of ψ^ and η^ in equation (64) and (65), respectively. Thus, from (18) μ^ is bounded.

6. Simulation results

The proposed control approach is applied for the robust control of the electrically driven two-link elbow manipulator. The dynamic parameters of the robot and the motors’ parameters have been presented in Table. 1 and Table 2, respectively. The desired position trajectory for end-effector, as illustrated in Fig. 2, is formulated by

where x_d1 and x_d2 are given as

Fig. 2.

Desired Trajectory

Fig. 3.

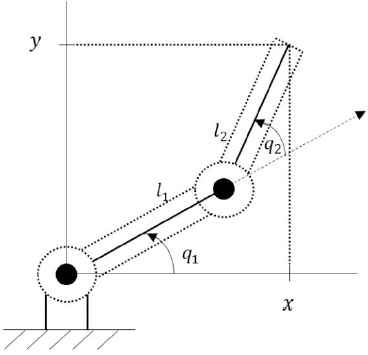
A two-link planar arm

Simulation 1. The environment model with x_e = [1.29 y]^T m and K_e = diag(100000,0) N ⁄ m is given by

where x_e ∈ R^m is the equilibrium position, and K_e is a n × n diagonal matrix which is called the stiffness of the environment. The model reference parameters in (25) are set to M_R = 5.4I₂ Ns² / m, B_R = 1500I₂ Ns / m and K_R = 500I₂ N ⁄ m. The control approach parameters are set to k₁ = diag(125,125), k₂ = diag(2.8,4), Γ = diag(0.01I₅, 0.1), γ_η = 0.1, σ = 0.2, δ = 0.1 by trial and error and the time delay is set to ε = 0.001 sec. The initial values for vector P^(0) are selected as P^(0)=1.1P . Furthermore, the parameters of fuzzy system are chosen as γ_f = 0.8 and σ_f = 0.55. The external disturbance profile &#x03C6;(t) is defined as a step function and is applied in t = 1.5 sec. The selected amplitude for external disturbance is chosen based on approximately 10% of the maximum voltage amplitude. The initial position for the end-effector is set to (x₀, y₀) = (−0.059 m, 1.259 m). The Schematic plot of robot manipulator trajectory is shown in Fig. 4. As shown in Fig. 4, the proposed controller should compensate the initial position of the end-effector to put it into the straight-line trajectory and finally the end-effector will interact the environment.

Fig. 4.

Schematic plot of robotic trajectory

The contact force between the end-effector and environment is depicted in Fig .5. As shown, the contact phenomenon occurs in 2.84 sec and the generated force reaches rapidly a maximum value of 122.1 N. From this time forward, the proposed compensator comes into operation and efficiently compensates the harmful effect of the contact and finally makes the contact force approximately decrease to 4 N.

Fig. 5.

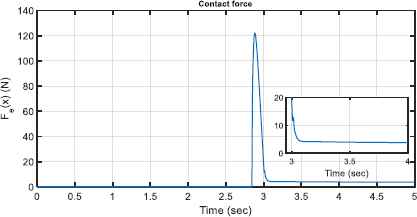
The contact force between the end-effector and environment

Motors behave well under the permitted voltages as shown in Fig. 6. The interaction effect of end-effector and environment for both motors’ voltages at t = 2.84 sec is detectable. Also, it is noted that from the contact between the end-effector and environment forward, both motors approximately tolerate constant voltages. Fig. 7 illustrates the performance of control approach providing similar behavior of robotic system and the reference model such that the reference errors are reduced well to the range of [–2.5 2.5] × 10⁻³ m. The tracking performance of the reference model is shown in Fig 8. The first reference model tracking error, i.e. x_d1 − x_m1, shows that the contact between the end effector and the environment occurs at t = 2.84 sec along the x axis. The second signal of reference model, x_m2, does not show any deviation from the desired signal, x_d2, since there is no force along the y axis. It is noted that by increasing the first model reference tracking error, the control approach protects the robot and the environment from the possible detrimental effect of the contact. To do this, according to Figure (5) and Figure (8), the contact force finally decreases to 4 N such that the second signal of reference model for the end-effector is deviated approximately 9mm along the x axis. Figure. 9 shows the adaptive fuzzy parameters (Eq. 64), ψ^=[ψ^1,…,ψ^27]T , which all parameters finally converge to constant values. The adaptation of η^ (Eq. 65) and P^ (Eq. 63) is also depicted in Fig. 10 and Fig. 11, respectively. The effectiveness of the proposed controller is shown by simulation results.

Fig. 6.

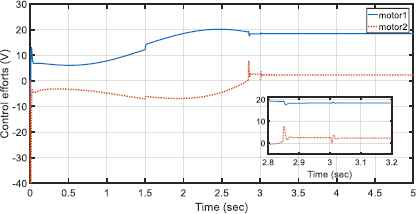
Control efforts of the proposed control approach

Fig. 7.

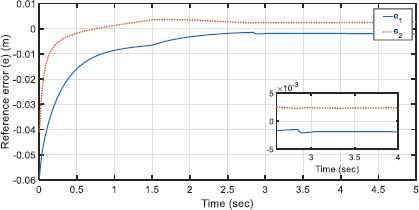
The reference errors (Eq. 34)

Fig. 8.

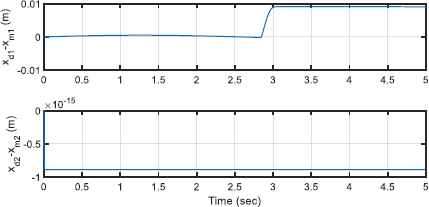
Tracking performance of the reference model

Fig. 9.

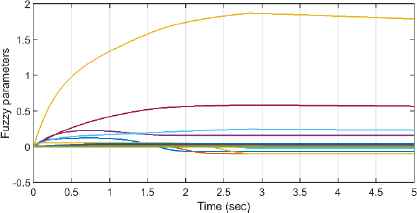
Adaptation of uncertainty fuzzy parameters

Fig. 10.

Adaptation of parameter η^

Fig. 11.

Adaptation of P^

Simulation 2. The performance of the proposed controller is evaluated by different stiffness of the environments. To perform simulation, four values for K_e are chosen as K_e1 = diag(20000,0), K_e2 = diag(60000,0), K_e3 = diag(100000,0) and K_e4 = diag(140000,0). Fig. 12 and Fig. 13 illustrate the contact force between the end-effector and different environments and the performance of the control method interacting with environments with different stiffness, respectively.

Fig. 12.

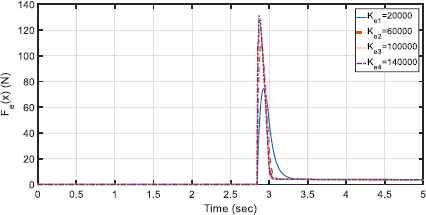
The contact force between the end-effector and environments with different stiffness

Fig. 13.

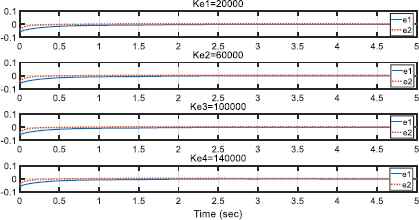
The performance of the control method interacting with environments with different stiffness

7. Conclusion

This paper has proposed a model-reference impedance control approach using fuzzy uncertainty estimator for the robust control of electrically driven robot manipulators. In the proposed control method, a desired dynamical behavior of the robot interacting with an environment is considered as the model-reference such that this model-reference provides a reference signal for a robot whether in tracking or contact situations. As the interaction between an end-effector and an environment occurs, the contact force is exerted to the model-reference and the robotic system receives the output of model-reference as a desired trajectory and thus the aim of the controller is to reduce the difference between the task space desired trajectory and the desired impedance model. It is worth noting that the feedback of contact force is not utilized in the structure of the proposed controller and the adaptive laws since by increasing the contact force at the time of the interaction between an end-effector and an environment, existing the contact force will cause problematic issues for control designers. Furthermore, to improve the performance of control system and also compensate un-modelled dynamics and external disturbances, two control terms namely a robustifying term and a fuzzy uncertainty estimator are employed in the structure of the controller. The proposed control approach has shown a good performance in terms of simplicity in design, high-performance of contact force compensation and small reference error. The stability analysis has been guaranteed by the proposed control method and the simulation results verified the effectiveness of the method.