Data-Intensive Service Provision Based on Particle Swarm Optimization
- DOI
- 10.2991/ijcis.11.1.25How to use a DOI?
- Keywords
- data-intensive service provision; ant colony optimization; genetic algorithm; particle swarm optimization
- Abstract
The data-intensive service provision is characterized by the large of scale of services and data and also the high-dimensions of QoS. However, most of the existing works failed to take into account the characteristics of data-intensive services and the effect of the big data sets on the whole performance of service provision. There are many new challenges for service provision, especially in terms of autonomy, scalability, adaptability, and robustness. In this paper, we will propose a discrete particle swarm optimization algorithm to resolve the data-intensive service provision problem. To evaluate the proposed algorithm, we compared it with an ant colony optimization algorithm and a genetic algorithm with respect to three performance metrics.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Data-intensive science is emerging as the fourth scientific paradigm, and new techniques and technologies for the new scientific paradigm are needed.1 As a result, applications based on data-intensive services have become one of the most challenging applications in service oriented computing and cloud computing.2,3 The authors of Ref. 4 presented a survey of the challenges, techniques, and technologies of data-intensive applications. For data-intensive applications, a variety of services for data mining, data storage, data placement, data replication, data transfer, and data movement have been deployed in distributed computing environments. To compose these data-intensive services will be more challenging, especially in terms of autonomy, scalability, adaptability, and robustness.
Ref. 4 proposed that bio-inspired computing was one of the potential techniques to solve the data-intensive problems. The authors stated that biological computing models were better appropriate for data-intensive problems because they had mechanisms with high-efficiency to organize, access, and process data. The authors of Ref. 5 already proved that it was useful for service management and discovery to add biological mechanisms to services. In our previous work,6 we have presented a hierarchical taxonomy of Web service composition approaches and provided a detailed analysis of each approach. Then we found that the bio-inspired algorithms could overcome the challenging requirements of the data-intensive service provision. It is useful for the provision of data-intensive services to explore key features and mechanisms of biological systems.
In this paper, we propose a discrete particle swarm optimization(PSO) algorithm to deal with the data-intensive service provision problem. Then the performance of the proposed algorithm is compared with an ant colony optimization(ACO) algorithm and a genetic algorithm(GA).
The remainder of the paper is organized as follows. In the next section, the related work is given. Section 3 introduces the data-intensive service provision problem and the particle swarm optimization algorithm. Section 4 presents the experimental settings and numerical results. Finally, section 5 concludes this paper.
2. Related Work
The process of developing a composite service is called service composition.7 Service composition can be performed by composing either component Web services or composite services. The component Web services are developed independently by different service providers, so some services may have same functionality but differ in quality of service (QoS) attributes as well as other non-functional properties. In the context of Web service composition, abstract services are the functional descriptions of services, and concrete services represent the existing services available for potential invocation of their functionalities and capabilities. Given a request of composite service, which involves a set of abstract services and dependency relationships among them, there is a list of service candidate sets, which includes many concrete services for each abstract service. Web service selection refers to finding one service candidate to implement each abstract service according to users’ requirements, which is an important part of Web service composition. For each abstract service of a composite service, the service composition process is to bind one of its corresponding concrete services and meet the constraints specified for some of the QoS attributes.8 The final goal of the composite service construction is achieved by solving the well-known service composition problem.
In the past ten years, bio-inspired algorithms such as the ACO algorithm, the GA, and the PSO algorithm have been used to solve the Web service selection and composition problem. The ACO algorithm is a probabilistic technique proposed by Dr. Marco Dorigo in 1992 in his PhD thesis. It is widely used for solving combinatorial optimization problems which can be reduced to finding good paths through graphs. The authors of Ref. 9 used different pheromones to denote different QoS attributes. Ref. 10 modeled the Web service selection problem as a multi-objective optimization problem, and proposed a multi-objective chaos ACO algorithm to solve it. Ref. 11 integrated the max-min ant system into the framework of culture algorithm to solve the Web service selection problem.
The GA belongs to the larger class of evolutionary algorithms, which generate approximate solutions to optimization and search problems using techniques inspired by the principles of natural evolution: selection, crossover, and mutation. The original GA was invented by Dr. John Holland in 1975. The authors of Ref. 12 proposed a GA with static and dynamic penalty strategies in the fitness function. Ref. 13 designed a repair GA to address the Web service composition problem in the presence of domain constraints and inter service dependencies. Ref. 14 proposed a GA to conduct the service composition, in which considering quantitative and qualitative non-functional properties.
The PSO is one of the evolutionary computational techniques developed by Dr. Eberhart and Dr. Kennedy in 1995, which was inspired by the social behavior of bird flocking and fish schooling. The PSO algorithm finds the optimal solution through iterations after initializing a group of random particles. Zhang15 proposed a QoS-aware Web service selection approach based on particle swarm optimization. Kang and so on16 transformed the Web service selection problem into a multi-objective optimization problem with global QoS constraints, then introduced a particle swarm optimization algorithm to solve it. Ref. 17 presented a hybrid algorithm that combined the Munkers algorithm with particle swarm optimization to solve the Web service composition problem.
In our previous work,18 we have presented a survey on bio-inspired algorithms for Web service composition. We also conducted a systematic review19 on the current research of Web service concretization based on ACO algorithms, GAs, and PSO algorithms. The data-intensive service provision is characterized by the large of scale of services and data and also the high-dimensions of QoS. However, most of the existing works failed to take into account the characteristics of data-intensive services and the effect of the big data sets on the whole performance of service provision. In this paper, we will investigate the applications of the particle swarm optimization algorithm to solve the data-intensive service provision problem.
3. Data-Intensive Service Provision Based on PSO
3.1. Problem Statement
3.1.1. Data-Intensive Service Provision Problem
The data-intensive service composition problem is an extension of the traditional service composition problem, in which data sets as inputs and outputs of services, are incorporated. The problem is modeled as a graph, denoted as G = (V,E,D), as shown in Fig. 1, where V = {AS1,AS2,…,ASn} and E represent the vertices and edges of the graph respectively, D = {d1, d2,…,dz} represents a set of z data servers. Each edge (ASi, ASj) represent a relationship between ASi and ASj. Each abstract service ASi has its own service candidate set csi = {csi,1,csi,2,…,csi,m},i ∈ {1,…,n}, which includes all concrete services to execute ASi. Each abstract service ASi requires a set of data sets, denoted by DTi, that are distributed on a subset of D. A binary decision variable xi,j is the constraint used to represent only one concrete service is selected to replace each abstract service during the process of service composition, where xi,j is set to 1 if csi,j is selected to replace abstract service ASi and 0 otherwise.
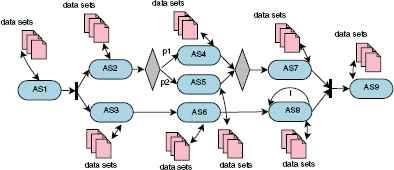
An example of graph for data-intensive service provision.
For simplicity, it is assumed that all data sets needed by each service have already been distributed in data centers prior to service composition following a uniform distribution. In addition, we will only consider the cost and response time of data-intensive services.
3.1.2. QoS Model
Consider a data-intensive service
The variable tcost is the cost of data transfer per time unit, bw(ddt, y) is the network bandwidth between data server ddt and service platform y, and size(dt)/bw(ddt, y) denotes the practical transfer time.
The estimated execution time for service
The variable sp(ddt) is the storage media speed of ddt, and nr is the number of data requests waiting in the queue prior to the underlying request for dt. The data transfer time depends on the network bandwidth and the size of the data. The storage access latency is the delayed time for the storage media to serve the requests, and it depends on the size of the data and storage type.20 Each storage media has many requests at the same time and it serves only one request at a time. The current request needs to wait until all requests that are prior to it have finished.
3.1.3. Utility Function
Suppose a composite service CS is composed of n abstract services, and there are m concrete services to implement each abstract service. Each concrete service csi,j is associated with a QoS vector
There are two phases in applying SAW: 1) the scaling phase is used to normalize all QoS attributes to the same scale, independent of their units and ranges; 2) the weighting phase is used to compute the utility of each service candidate by using weights depending on users’ priorities and preferences. For negative QoS attributes, values are scaled according to (3). For positive QoS attributes, values are scaled according to (4).
In (3) and (4),
Furthermore,
The function F denotes the aggregation function of the k-th QoS attribute, which could refer our previous work.18
In addition, we use
The utility function for a concrete service csi,j is computed according to (7).
Here, Wk ∈ [0,1] and
The utility function for a composite service CS is also computed according to the SAW method, which is similar to (3)–(7). When scaling the aggregated values of QoS attributes for a composite service, the numerators of (3) and (4) should be replaced by (8) and (9).
Here,
3.2. Data-Intensive Service Provision Based on PSO algorithm
3.2.1. The standard PSO algorithm
PSO has been widely used to solve optimization problems because it is very robust, and it is simple and easy to implement. It uses a population of particles that fly through the search space of the problem with given velocities. The velocity of a particle determines the direction and distance of its evolution. Each particle i corresponds to a possible solution of the problem. The position of each particle is determined by a d-dimensional vector
The particles update their positions and velocities according to (10).
The variable ω is the inertia weight that controls the exploration and exploitation of the search space. γ1 and γ2 are two mutually independent random numbers. The variables c1 (cognition coefficient) and c2 (social coefficient) are the acceleration constants,24 which change the velocity of particle i towards
The following procedure can be used for implementing the PSO algorithm.
- 1
Initialization. The swarm population is formed.
- 2
Evaluation. The fitness of each particle is evaluated.
- 3
Modification. The best position of each particle, the velocity of each particle, and the best position of the whole swarm are modified.
- 4
Update. Each particle is moved to a new position.
- 5
Termination. Steps 2–4 are repeated until a stopping criterion is met.
The standard PSO approach is commonly used on real-valued vector spaces, and can also be applied to discrete-valued problems where either binary or integer variables have to be arranged into particles.24 When integer solutions (not necessarily 0 or 1) are needed, one way is to round off the real optimum values to the nearest integer,25 and the other way is to define new operations and entities of the PSO approach. For example, in a discrete PSO approach, the velocity’s update is randomly selected from the three parts in the right-hand side of Eq. (10), using probabilities depending on the value of the fitness function.24 Inspired by Ref. 26, in the following section we will redefine operations and entities of Eq. (10) to adapted the PSO algorithm to solve the service composition problem.
3.2.2. The proposed discrete PSO algorithm
The first key issue when designing the PSO algorithm lies in its particle representation that related to the problem hyperspace. In order to construct a direct relationship between the domain of the service composition problem and the PSO particles, d numbers of dimensions are presented n abstract services in the composition process. Hence, each particle i corresponds to a candidate solution of the service composition problem. The location of a particle in the d-th dimension represents the concrete service which the d-th abstract service selects. Fig. 2 shows a particle representation for a service composition problem with nine abstract services and each has one hundred concrete services.

Illustration of a particle’s solution.
The fitness function of the PSO algorithm is the utility function which presented in section 3.1.3. Formally, the optimization problem in this paper is described as follows. Find a solution CS in graph G by replacing each abstract service ASi in V with a concrete service csi,j ∈ csi such that the overall fitness UCS is maximized with the constrained condition.
The process of generating a new position for a selected particle in the swarm is depicted in Eq. (11).
The definitions of the operators, used in the body of Eq. (11) are as follow.
The subtract operator (⊖). Differences between a desired position
The add operator (⊕). This operator is a crossover operator that typically is used in GAs. We select two cut points from the current position

Illustration of the manner in which ⊕ operator performs.
As it seems, the proposed equations have all major characteristics of the standard PSO equations. The coefficient is a vector of ones. The following pseudo-code describes in detail the steps of the proposed PSO algorithm.
| 1 | t = 0; |
| 2 | for i = 1 to swarm size |
| 3 | Initialize
|
| 4 |
|
| 5 | end for |
| 6 | calculates the fitness value of each particle
|
| 7 |
|
| 8 | while 1 |
| 9 | for i = 1 to swarm size |
| 10 | update velocity and position using (11); |
| 11 | calculates the fitness value
|
| 12 | if
|
| 13 |
|
| 14 | else |
| 15 |
|
| 16 | end if |
| 17 | end for |
| 18 | if
|
| 19 |
|
| 20 | end if |
| 21 | t←t +1; |
| 22 | if stopping criteria are true |
| 23 | break; |
| 24 | end if |
| 25 | end while |
| 26 | return
|
4. Computational experiments
4.1. Evaluation method and the dataset
In this section, we investigate a comparison study on the effectiveness of the proposed PSO algorithm, the ACO algorithm27 and the GA28 by solving the data-intensive service composition problem. The experimental frameworks involves two influencing variables: the number of abstract services in the com posite service, and the number of concrete services for each abstract service. Here, the influence of the number of data sets is not considered.
For the purpose of the evaluation, different scenarios are considered where a composite service consists of n abstract services, and n varies in the experiments between 10 and 50, in increments of 10. There are m concrete services in each service candidate set, and m varies in the experiments between 100 and 1000, in increments of 100. Each abstract service requires a set of k data sets, and k is fixed at 10 in the experiments. A scenario generation system is designed to generate all scenarios for the experiments. The system first determines a basic scenario, which includes sequence, conditional and parallel structures. With this basic scenario, other scenarios are generated by either placing an abstract service into it or adding another composition structure as substructure. This procedure continues until the scenario has the predefined number of abstract services.
Three performance factors were evaluated: 1) the required computation time; 2) the quality of the solution; and 3) the value of OptIT, which is the number of the iterations when the best utility appeared, and from this iteration the best utility will not change until the termination condition has been reached. As PSO, ACS and GA are sub-optimal, the solutions obtained by these three bio-inspired algorithms have been evaluated through comparing them with the optimal solutions obtained by the mixed integer programming (MIP) approach.22,29 The open source integer programming system lpsolve version 5.5.2.530 was used for the MIP approach.
The number of ants in the ACO27, the population in the GA28, and the number of particles in PSO is all set to 100. And the maximum number of iterations is set to 1000. The synthetic datasets were experimented. For each scenario, the price of a data set, the network bandwidth (Mbps) between each data server and the service platform, the storage media speed (Mbps), the size (MB) of a data set, and the number of data requests in the waiting queue were randomly generated from the following intervals: [1,100], [1,100], [1,100], [1000,10000] and [1,10]. Then every scenario was performed with 50 runs. All runs of the same scenario use the same data, and the average results over 50 independent runs are reported. All the experiments are conducted on MAT-LAB 7.13.0.564 and executed on a computer with Inter(R) Core(TM) i7-6700HQ CPU 2.6GHz with 16GB of RAM.
4.2. Results Analysis
One example of all experiments is given to show the evolution of fitness value over the PSO iteration, which is shown in Fig. 4. The figure shows a scenario where a composite service consists of 10 different abstract services, and each abstract service has 200 service candidates. In the figure, the short blue line represents the global best fitness value in the current iteration. The results indicate that the PSO could find the best fitness in the second iteration.

The evolution of
In Fig. 5 and Fig. 6, the computation time of PSO, ACS, GA, and MIP are compared with respect to the number of candidate services and the number of abstract services. In Fig. 5, the number of candidate services for each abstract service varies from 100 to 1000, while the number of abstract service is set to 10. The results indicate that the proposed PSO is faster than other methods. By increasing the number of candidate services, the required computation time of PSO increases very slowly, this makes PSO be more scalable. In Fig. 6, the number of abstract services varies from 10 to 50, while the number of candidate services for each abstract service is fixed at 100. The results of this experiment indicate that the performance of all methods degrades as the number of abstract services increases. Again, we observe that PSO outperforms others. The reason is that we adopt a local selection approach in the add operator of our discrete PSO algorithm.

The computation time of PSO, ACS, GA, and MIP vs. number of candidate services

The computation time of PSO, ACS, GA, and MIP vs. number of abstract services
Furthermore, after collecting all the results of the scenarios, we find that the fitness value of the final best solution obtained by PSO, ACS, GA in all scenarios are the same with that of the MIP approach. In other words, the results show that all the three bio-inspired algorithms are able to achieve the optimal solutions. That’s because we use
We also compared the mean of OptIT values obtained by PSO, ACS and GA with respect to a varying number of candidate services and a varying number of abstract services. When the number of abstract services is fixed at 10, as the number of concrete services increases from 100 to 1000, the mean of OptIT values obtained by PSO, ACS and GA are 2, 1 and 5 in all scenarios, respectively. That is to say, the three bio-inspired algorithms found the best fitness value in the fixed iteration, and it does not change as the number of concrete services increases. When the number of concrete services is fixed at 100, as the number of abstract services increases from 10 to 50, the mean of OptIT values obtained by PSO is 2 for all scenarios, the mean of OptIT values obtained by ACS is 1, 1, 1, 1, 3 for each scenario, and the mean of OptIT values obtained by GA is 5, 8, 10, 11, 12 for each scenario. The results show that ACS and GA need more iterations to get the best fitness value.
5. Conclusion
In this paper, we present and evaluate a discrete particle swarm optimization algorithm to support the data-intensive service composition. The composition problem is modeled as a directed graph. Replacing the classical operators in the standard particle swarm optimization algorithm, we proposed equations analogous to them. In our discrete version of particle swarm optimization, the representation of the position and velocity of the particle is integer vector, by which we accomplished the mapping between the concrete service selection and the particle. The algorithm adopts a local selection method and a two-point crossover operation to find the optimal solution. Comparisons with the ant colony optimization algorithm, the genetic algorithm, and the mixed integer programming approach show the scalability and effectiveness of our proposed algorithm. For future work, extension of the proposed approach will apply for solving multi-objective and dynamic data-intensive service composition problem.
Acknowledgments
This work has been supported by National Natural Science Foundation of China under Grant No. 61702398 and No. 61502370, Natural Science Ba sic Research Plan in Shaanxi Province of China (Program No.2016JQ6003), China 111 Project under Grant No.B16037, and the Fundamental Research Funds for the Central Universities under Grant No.XJS15045.
References
Cite this article
TY - JOUR AU - Lijuan Wang AU - Jun Shen PY - 2018 DA - 2018/01/01 TI - Data-Intensive Service Provision Based on Particle Swarm Optimization JO - International Journal of Computational Intelligence Systems SP - 330 EP - 339 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.25 DO - 10.2991/ijcis.11.1.25 ID - Wang2018 ER -
