International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 12, Issue 2, 2019, Pages 1613 - 1621

Character-Level Quantum Mechanical Approach for a Neural Language Model

Authors
Zhihao Wang1, *, Min Ren2, Xiaoyan Tian3, Xia Liang1
1School of Management Science and Engineering, Shandong University of Finance and Economics, Jinan 250014, China
2School of Mathematics and Quantitative Economics, Shandong University of Finance and Economics, Jinan 250014, China
3Shandong Police College, Jinan 250014, China
*Corresponding author. Email: wzh861125@hotmail.com
Corresponding Author
Zhihao Wang
Received 22 April 2019, Accepted 9 November 2019, Available Online 25 November 2019.
DOI
10.2991/ijcis.d.191114.001How to use a DOI?
Keywords
Character-level; Quantum theory; Network-in-network; Language model
Abstract

This article proposes a character-level neural language model (NLM) that is based on quantum theory. The input of the model is the character-level coding represented by the quantum semantic space model. Our model integrates a convolutional neural network (CNN) that is based on network-in-network (NIN). We assessed the effectiveness of our model through extensive experiments based on the English-language Penn Treebank dataset. The experiments results confirm that the quantum semantic inputs work well for the language models. For example, the PPL of our model is 10%–30% less than the states of the arts, while it keeps the relatively smaller number of parameters (i.e., 6 m).

Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

Languages are used to convey meaning, so the ultimate goal of natural language processing (NLP) research is to represent the meaning of an utterance in computers. In recent years, a series of semantic models has been proposed for NLP. These semantic models can mimic human thinking to a certain extent and can solve problems in the real world. Although each model has its own detailed characteristics, they all use text collections as input for the model and a vector space to represent words or concepts. With the development of deep learning technology, distributed word representation has become one of the main methods of text representation. Relatively speaking, this form of representation is more condensed and has fewer dimensions, but it is sufficient to represent the elements in space. For example, Bengio et al. [1] proposed a language model that is constructed using a three-layer neural network. Based on this approach, Mnih and Hinton [2] proposed a hierarchical idea to eliminate the most resource-consuming matrix multiplication from the last hidden layer to the output layer, thereby accelerating the process while retaining the performance. Distributed word representation has achieved the most remarkable results to date. In more recent research, it is believed that information about word morphology and shape is normally ignored when learning word representations. Based on this idea, Santos et al. [3] proposed a character-level representation of words and combined it with a distributed word representation to implement the application of voice tags. Later, LeCun et al. [4] proposed a method for learning the distributed character representation directly through character learning without prior distributed word representation training. Their study found that the distributed character representation performed very well in large-scale corpus sets. Kim et al. [5] used the distributed character representation to implement language modeling, and this method could be used in different languages.

Several of the abovementioned distributed character representations are obtained through convolutional neural network (CNN) training. CNNs have achieved state-of-the-art results in computer vision and have been shown to be effective for various NLP tasks. CNNs have the properties of location invariance and compositionality, which is why CNNs play an important role in computer vision. However, the application of CNNs in NLP is different from their use in computer vision. Neighboring pixels in an image are often related (i.e., belong to the same part of an object), but the words might not be the same. In many languages, phrases are segregated by many other words. Additionally, one must pay attention to a word's position in a sentence, so location invariance is not applicable in NLP problems. Similarly, the composability can be unclear. It is obvious that the words are combined together in certain ways, such as using adjectives to modify nouns or using adverbs to modify verbs or adjectives. However, it is not as obvious as computer vision when interpreting the meaning of more advanced features. In the current distributed character representation research, the characters in the CNN's input are all encoded using one-hot or similar methods. This type of coding method is simple but does not provide an intuitive feeling as the image pixels do. However, when considering natural language, does the human brain always read in order? In much of the current research on speed reading [6], the methods that are used to understand and remember words are based on the way in which people recognize images. Therefore, if language coding can reflect more of this rule, then the performance of language models might be greatly improved. As we all know, language is the result of neuron activities in the human brain. If classical physics can be considered an extreme case of quantum mechanics, then the brain can be considered a measuring device with a quantum computing system. Then, language interpretation can be considered a quantum measurement process [7].

The NLP based on quantum theory is a new research idea that differs from distributional semantics representation. The quantum language model encodes the probability uncertainties of both single and compound terms in a density matrix, without extending the vocabulary [8]. In the quantum language model, each text term is represented by a density matrix that is a one-hot vector. The density matrix only encodes the local occurrence without taking into account the global semantic information. Furthermore, a density matrix is calculated via an iterative process, instead of an analytical procedure. Thus it is difficult to integrate such matrix into an end-to-end deep neural network [9].

In order to address the above problem, we use character-level embedding to represent text to encode richer semantic information than one-hot vector. We use an eigenstate of quantum theory to represent the characters, the superposition of eigenstates to represent words, unitary operator to represent phrases. Therefore, a long text is represented by a mixed state and hence it can be integrated into a neural network. The language models can be used in NLP research fields such as machine translation, question and answer, and text classification.

In the following, we use the mathematical framework of quantum theory to construct a semantic information model. Specifically, the model describes how quantum states can be used to represent characters, words, and even sentences. The resulting language representation then serves as the CNN input, thus achieving the goal of text classification. The present study makes contributions in four main aspects as follows:

  • We proposed a character-level quantum neural language model (NLM) that does not require word order or syntax information. It implements language representations with rich semantic and orthographic features through character-level coding. Therefore, this method does not need to pre-process the text data for morphological annotation, nor to use pre-trained embedding representation in the input layer.

  • A CNN is applied to distributed or discrete embedding without knowing the syntactic or semantic structure of languages.

  • In order to reduce the overfitting risk and computational load, we introduce a network-in-network (NIN) model into the network to reduce the number of parameters and computation cost.

  • The experiments show that our proposed model achieves the performance of state-of-the-art on the English-language Penn Treebank (PTB) dataset with fewer parameters.

The rest of this paper is organized as follows: Sections 2 and 3 discusses related work and preliminary. Next, we introduce the related mathematical background of quantum theory in Section 4 and propose the quantum semantic space model. In Section 4, the character-level CNN language model is given and quantum semantic feature learning is conducted. The experimental results and analysis are given in Section 5. Finally, the study is concluded in Section 6.

2. RELATED STUDIES

2.1. Neural Language Model

NLM research has made remarkable progress. Various structure models, including feed-forward [1], RNN [10], log-bilinear [11], sum-product Net [12] and CNN [13–15], have achieved state-of-the-art results.

Two main methods are used in the study of natural language semantic representation: distributed word representation models based on n-gram language models [16] and character-level NLMs. N-gram models are language-independent and have advantages such as the ability to handle text in different languages at the same time, not requiring linguistic processing for the text, being tolerant of spelling mistakes, no lexicon or rules required, and fewer text feature dimensions [17]. Bilmes et al. [18] proposed a count-based n-gram language model to represent words as a set of shared factor embeddings. Based on this approach, Alexandrescu et al. [19] proposed the factored neural language model (FNLM) to solve the rare word problem. FNLM can make better use of morphemes, word shape information, and other tags to represent words. FNLM quickly became a popular research topic. Luong [20], Botha [21], and Qui et al. [22], proposed different types of FNLMs for learning morpheme embedding representation. These models can make better use of morphemic information by representing words as a function of their own morpheme embeddings. Word embeddings have become the most widely used mainstream method for natural language semantic representation. Character-level NLM is another research idea that has recently become popular. The inputs and outputs of these models are characters [23,24]. Character-level models do not consider any morphological tagging or manual feature engineering. The latest series of studies has shown that these models performance is usually superior to that of word-level models [4,5].

CNNs [25] are useful in extracting information from raw signals. They have been successfully used in computer vision research area. In recent years, CNNs have been shown to be effective for various NLP tasks. However, the architectures used for NLP applications are different because they typically involve temporal rather than spatial convolutions [4,5]. They consider the character-level text as the raw signal, an applying temporal (one-dimensional) convolutional networks to it. In the temporal convolutional module, the main components are 1-D convolution layers [4]. Similar to zhang [4], Prusa et al. [26] also proposed a character embedding to create a more compact data representation, reducing training time and memory requirements. The main shortcoming of character-level Language Models which use of a vanilla convolutional network like zhang [4] and Prusa [26] is the receptive field of each convolutional layer is often small that the network must very deep in order to capture long-term dependencies in an in-put text. Thus, Kim et al. [5] and Xiao et al. [27] proposed hybrid methods of convolutional and recurrent networks.

2.2. Quantum-Theoretic Approach to NLP

The NLP based on quantum theory is a new research idea that differs from natural language distributional semantics representation. The above studies focused on word- or character-level distributional semantic representation. It is very difficult to extend these methods to the sentence level. Quantum states can conveniently represent words and sentences. Aerts et al. [28] and Bruza et al. [29] first attempted to use quantum theory as a mathematical basis for semantic space models. Aerts proved that latent semantic analysis (LSA) model [30] is essentially a series of Hilbert space formalisms. Bruza confirmed that the Hyperspace Analogue to Language (HAL) model [31] also conforms to Hilbert space formalisms and designs lexical operators through corpus co-occurrence counts. Grefenstette et al. [32] proposed a semantic combination model based on a quantum theoretical context; however, this method does not utilize the unique aspects of quantum theory. Blacoe et al. [33] used quantum theory as a standard framework to implement a semantically aware semantic space model that captures lexical meaning. This method establishes density matrices by grammatical dependencies, considers word ordering and utilizes important concepts in quantum theory, such as superposition and entanglement (more details see Section 4).

3. PRELIMINARY

3.1. Quantum Semantic Space Model

In quantum mechanics, the state of the system can be represented by a complex vector, described by the ket-bra symbol, recorded as |a〉 called ket vector. The ket vector is a column vector, and the row vector is written in the form of 〈•|, which is called a bra vector. The α† is called the adjoint of α and there is a special kind of linear operator which called the Hermitian that satisfies ξ†=ξ. It is a counterparts of the real numbers in operators. In quantum mechanics, all meaningful dynamical variables in quantum physical systems are represented by Hermitian operators called observables. For an Hermitian operator (an observable) ζ, there is a set of kets (or states) that satisfies Equation (1)

ξ|x〉=λ|x〉
with λ∈ℝ and |x〉≠0. The ket |x〉 is the eigenstate of ξ and λ is the eigenvalue of ξ. Eigenvalues can be either discrete or continuous, and the norm of the corresponding eigenstate is equal to one.

There is a class of operators which defined as Equation (2) that preserve the norm of kets.

|p′〉=U|p〉
where 〈p′|p′〉=〈p|p〉 and U is called unitary operator which is an operator with the property
U†U=UU†=I
where I is the identity operator and I|x〉=|x〉.

A quantum mechanical system is linear. That is, if |x1〉 and |x2〉 are both physical states allowed by a particular quantum system, a superposition of them |x′〉=c1|x1〉+c2|x2〉 with c1,c2∈ℂ being complex numbers. A quantum state such as |x〉, which can be directly described by a ket, is called a pure state, and a quantum state composed of different pure states according to statistical probability is called a mixed state. The mixed state is represented by the density matrix which defined as Equation (3)

ρ=∑ipi|xi〉 〈xi|
where pi indicates the probability that the quantum system is in pure state |xi〉, which is non-negative and does not need to satisfy ∑ipi=1. The density matrix is self-adjoint, semi-positive (positive semi-definite), and its trace is one.

3.2. Convolutional Neural Network

3.2.1. The basic components

The basic components of CNN consist of three types of layers, namely convolutional, pooling, and fully-connected layers. The convolutional layer which is composed of several convolution kernels aims to learn feature representations of the inputs. The convolution kernel of convolutional layer which is used to compute different feature maps is shared by all spatial locations of the input to generate each feature map. The complete feature maps are obtained by using several different kernels. Mathematically, the feature value at location (i,j) in the kth feature map of lth layer, zi,j,kl, is calculated by Equation (4).

zi,j,kl=wklTxi,jl+bkl
where wkl and bkl are the weight vector and bias term of the kth filter of the lth layer respectively, and xi,jl, j is the input patch centered at location (i,j) of the lth layer. In order to enable the multi-layer network to have the ability to detect nonlinear features, the nonlinear function is introduced into the CNN through the activation function. Let a(⋅) denote the nonlinear activation function. The activation value ai,j,kl of convolutional feature zi,j,kl can be computed as Equation (5).
ai,j,kl=azi,j,kl

Typical activation functions are sigmoid, tanh and ReLU [34].

The pooling layer which is usually placed between two convolutional layers aims to achieve shift-invariance by reducing the resolution of the feature maps. Let p(⋅) denote the pooling function. The pooling value yi,j,kl for each feature map a:,:,kl can be computed as Equation (6)

yi,j,kl=pam,n,kl,∀(m,n)∈ℛij
where ℛij is a local neighborhood around location (i,j). The typical pooling operations are average pooling and max pooling [34].

After several convolutional and pooling layers, there may be one or more fully-connected layers which aim to perform high-level reasoning. Let θ denote all the parameters of a CNN. The optimum parameters for a specific task can be obtained by minimizing an appropriate loss function defined on that task. Suppose there are N desired input-output relations {(x(n),y(n));n∈[1,⋯ ,N]}, where x(n) is the n-th input data, y(n) is its corresponding target label and o(n) is the output of CNN. The loss of CNN can be calculated as Equation (7).

L=1N∑n=1Nl(θ;y(n),o(n))

Training CNN is a problem of global optimization. By minimizing the loss function, we can find the best fitting set of parameters. Stochastic gradient descent is a common solution for optimizing CNN network [34].

3.2.2. CNN for NLP

The architectures used for NLP applications are different from the basic CNN because they typically involve temporal rather than spatial convolutions [4,5]. Suppose there is a discrete input function g(x)∈[1,l]→ℝ and a discrete kernel function f(x)∈[1,k]→ℝ. According to Zhang [4], convolution h(y)∈[1,[(l−k+1)∕d]]→ℝ can be defined as Equation (8).

h(y)=∑x=1kf(x)⋅g(y⋅d−x+c)
where c=k−d+1 is an offset constant.

3.2.3. Network in network

NIN is a general network structure proposed by Lin et al. [35]. It replaces the linear filter of the convolutional layer by a micro network called mlpconv layer which makes it capable of approximating more abstract representations of the latent concepts. The overall structure of NIN is the stacking of mlpconv layer. The computation performed by mlpconv layer is formulated as Equation (9):

ai,j,knn=maxwknTai,j,:n−1+bkn,0
where n∈[1,N], N is the number of layers in the mlpconv layer, ai,j:0 is equal to xi,j.

4. OUR MODEL

4.1. Semantic Space Model Inspired by Quantum Theory

In quantum theory, the state of a physical system can be described as superposed eigenstates, and the eigenstates are orthogonal. Any state, including eigenstates, can be represented as a complex number vector. Assuming that ℂn is a finite-dimensional complex vector space, then the column vector ψ →∈ℂn can be expressed as Equation (10).

ψ→=ψ1ψ2⋮ψn=ψ1v→1+ψ2v→2+⋯+ψnv→n
where B=v→1,v→2,⋯,v→n is a basis vector of the vector space. The corresponding state can be represented more conveniently using bra-ket notation [36]. The corresponding column vector is called ket and is denoted as |ψ〉, and the row vector is called bra and denoted as 〈ψ|; 〈ψ|=|ψ〉†=|ψ〉∗. The superscript * indicates a complex conjugate, and the superscript t is the transpose operator.

Definition 1

A language formulation representation L is a quantum morphism operator:

L:B→L

B is the basis vector, and L is the symbol in the lexicon. L=ψ|l〉, and ψ∈ℝ is the eigenvalue of L. For each lm,ln∈L and lm≠ln, 〈lm|ln〉=0. That is, all of the symbols in L are orthogonal to one another. In other words, the states in L are pure states. In the description of a quantum system, the quantum state used to represent natural language is the superposition of the eigenstates of a particular alphabet's eigenbasis. Therefore, the bra-ket notation used to represent a natural language's quantum state is shown in Equation (11).

|ψ〉≡ψ→=∑nψn|vn〉

In the equation, vn is the eigenstate and represents a character (letter). ψn=vnψ represents mapping ψ into vn, and ψn denotes the probability amplitude. To facilitate the application of quantum theory in natural language representation, the complex number ψn is written in polar form according to Eulers formula, ψn=rneiθ. Then, Equation (11) can be expressed as Equation (12).

ψ=∑nrneiθnvn
where rn and θn represent the module and phase of the complex coefficient, respectively.

Inspired by the literature [4], we used the “one-hot” complex code C as the character table. Please refer to the character coding table in Reference [12], which consists of 70 characters, including 26 English letters, 10 digits, 33 other characters, and the new line character. The non-space characters are

a b c d e f g h i j k l m n o p q r s t u v w x y z 0 1 2 3 4 5 6 7 8 9- , ; . ! ? : ’ ’ ’/ \ | _ @ # $ % ^ & * ‘ + - = < > ( ) [ ] { }

When representing a natural language, |vn〉 represents a specific letter, and |ψ〉 represents a word. ψn is the eigenvalue of the corresponding letter (the occurrence of letters in the corpus was used in the present study). Taking the sentence “I like this movie very much” as an example, the word “like” can be expressed as |like〉=ψl|l〉+ψi|i〉+ψk|k〉+ψe|e〉. Further, to represent the phrase with an intrinsic logical relationship, “very much”, or even this particular sentence, it is necessary to introduce a unitary operator.

Definition 2

Unitary Operator: A bounded linear operator in Hilbert space H, U:H→H, is called a unitary operator. It satisfies U∗U=UU∗=I, where U∗ is the adjoint of U and I:H→H is an identity operator. Unitary transformations are linear isomorphisms.

The unitary operator U is shown in Equation (13).

Ut=e−iH′ℏt

Here, H′ denotes the Hamiltonian matrix [37], ℏ is the Dirac constant and t denotes the timing of the word occurrence, that is, the specific position of a particular word in the language representation. According to the definition of a unitary operator, it has the property of U†=UT∗=U. Namely, a unitary operator is an automorphism of the Hilbert space and can maintain the spatial structure. Therefore, Equation (14) can be derived.

ψU=∑m=1nUtmeiθmψm=∑m=1neiθm−Htmℏψm

Here, ψ1,ψ2,⋯,ψn is a string of eigenstates (e.g., like), n is the length of the string and tm is the timing of word m (the position of m in the string). For example, very much=eiθ1−5Hℏvery+eiθ2−6Hℏmuch.

Proof.

ψU=∑m=1neiθm−Htmℏψm

ForψU=∑m=1nUtmeiθmψm =∑m=1ne−iH′ℏtmeiθmψm, and a Hamiltonian matrix, H, the sum (and any linear combination) of two Hamiltonian matrices is also Hamiltonian.

So,ψU=∑m=1ne−iHℏtme−iH′ℏtmeiθmψm =∑m=1neiθm−Htmℏψm

In quantum mechanics, if the state of a system is certain, it is called a pure state. A pure state is a quantum state that can be directly described by a state vector ψ. The quantum state formed by several pure states according to statistical probabilities is called a mixed state and can be described by the density operator. The density matrix is a self-adjoint, and the positive semi-definite operator has a trace of one, as shown in Equation (15) [38].

ρ̂=∑NPNψNψN

Equation (15) shows that the probability that a quantum system is in the pure state of ψ1 is P1, that the probability of being in the pure state of ψ2 is P2 and that the probability of being in the pure state of ψN is PN. In this paper, PN is tf-idf. Here, ψ2 are not necessarily orthogonal to one another and do not need to satisfy ∑ipi=1.

Combining Equations (14) and (15) gives Equation (16)

ρ̂=∑NPNψNψN =∑NPN(∑m=1neiθm−Htmℏvm)N(∑m=1neiθm−Htmℏvm)N =∑NPN(∑m=1neiθm−Htmℏvmvm)N

In natural language representation, static text strings can be implemented using Equation (11). However, when processing a dynamic text stream, the semantics of the same word, phrase or sentence in different contexts can be different. Therefore, it is necessary to introduce the concept of a mixed state. For example, the statement “I like this song very much” in a static text can be described using the equation

I like this song very much=ψ1I+ψ2like+,⋯,+ψ5very much

A set of text symbols {I,like,this,song,very,much} in a dynamic text stream can be described as

ρ̂{I like this song very much}=P1ψIψI+ Plikeψlikeψlike+,⋯,+  Pvery muchψvery muchψvery much

Here, ψvery much=eiθ1−5Hℏvery+eiθ2−6Hℏmuch can be derived from Equation (14). We assume that {ψn} is a set of orthonormal bases that correspond to the elements ℘ij of the density matrix ℘ of the density operator, as shown in Equation (17).

℘ij=∑nPnviψnψnvj

4.2. Character-Level CNN Language Model Based on Quantum Mechanical

However, in the present study, the input data are density operators, and the potential connections among the data are fully considered in this type of representation. Compared with traditional text representation methods, this type of input data can be processed in a more intuitive manner that is more similar to processing pictures. Therefore, the main component of the CNN model that we adopted is the spatial convolutional module. The model structure is shown in Figure 1. The input is the density operator that represented text using the quantum semantic space model.

Figure 1

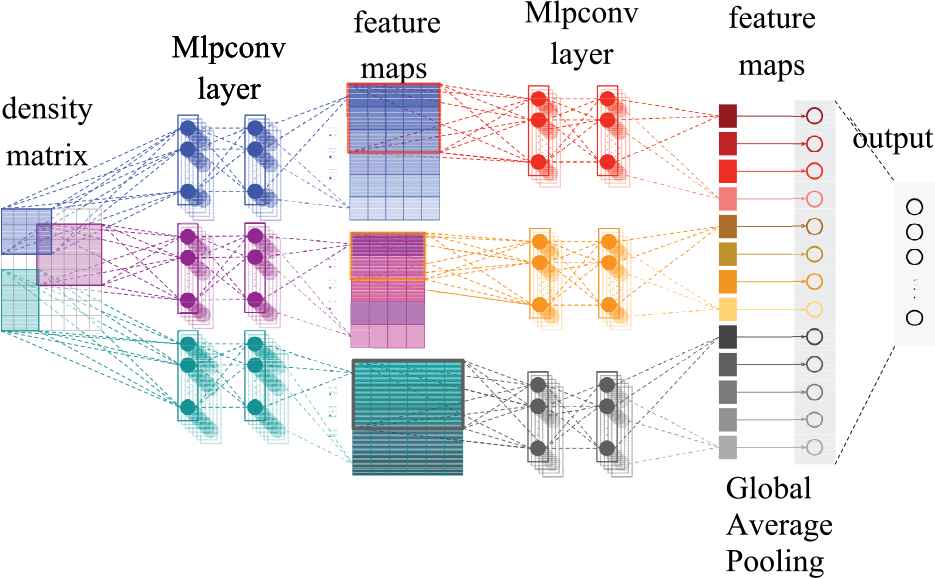
An example of a character-level convolutional neural network (CNN) language model with a two-layer network-in-network (NIN) structure. The input layer is a density operator. The convolution operation was conducted on two layers of mlpconv to obtain feature combinations that represented abstract concepts. Feature combinations went through GAP and were then input into the softmax layer for classification.

Let C be the vocabulary of characters, and let d be the dimension of character embeddings. Then, the inputted matrix character embeddings ℘∈ℂd×c are used as the density matrix of the character embeddings, where d = c = 70; that is, its size is related to only the dimension of the character embeddings. In the model architecture in this work, the convolutional layer uses a narrow convolution of width W and height H. Let f denote the feature map produced by the convolutional layer, which can be described as a three-dimensional W∗H∗N array, where N represents the number of filters.

To enhance the discrimination ability of the local receptive fields, the NIN model [35] was introduced into the model used in the present study. Its structure is shown in Figure 1. In a traditional CNN, a series of over-complete filters can be used to extract various potential features. However, this process requires too many parameters. Because the high-level features of the CNN are obtained by combining lower-level features, in NIN, the traditional generalized linear model (GLM) filter (mlpconv) in each local receptive field was replaced by a multi-layer perceptron (MLP) to generate concepts that are more abstract before combining low-level features into high-level features. By contrast, the last layer of a traditional CNN is a fully connected layer with many parameters and is prone to overfitting. Therefore, in the NIN, the last mlpconv layer outputs the spatial average of the feature map directly into the next layer for classification using global average pooling (GAP).

The layer structure of mlpconv is shown in Figure 1. It is essentially a general nonlinear function approximator. Thus, the a priori distribution of the potential concepts might not be required but could be obtained through local feature extraction using the universal function approximator. In this way, a more abstract conceptual representation can be achieved. The mlpconv can be trained using the entire network and backpropagation.

The calculation performed by the mlpconv layer is shown as follows:

f i,j,k11=max(ωk11Txi, j+bk1,0)⋮f i,j,k nn=max(ωknnTf i,jn−1+bkn,0)
where n is the number of layers in the multilayer perceptron and f is the activation function of the multilayer perceptron.

Unlike the traditional fully connected layer, in GAP, each feature map is globally pooled to generate an output. This pooling can greatly reduce the number of network parameters and avoid overfitting. In addition, each feature map is equivalent to an output feature, and this feature characterizes the output class. GAP can replace the fully connected layer because after passing through the mlpconv layer, each feature map represents high-level information that can be used for classification, detection or other tasks. Algorithm 1 shows the procedure of training the model.

Algorithm 1: Pseudo code for the training process.

1: procedure trainmodel(dataset, maxepoch, batchsize) Input: dataset is the PTB dataset we use to train and test the model; maxepoch is the max number of epoch; batchsize is the size of minibatch.

2:  model parameters ← randomly initialized

3:  for epoch ∈ 1,2,3,...,maxepoch do

4:    for minibatch ∈ dataset do

5:      Compute Loss

6:      Compute Gradient

7:      Update Parameters

8:    end for

9:  end for

10: end procedure

5. EXPERIMENTS

5.1. Dataset

For comparison with existing works [5,12,13,23,39–42], We conduct hyperparameter search, model introspection, and ablation studies on the English PTB. The PTB dataset is a large annotated corpus, which consists of 929k training words, 73k validation words, and 82k test words was used as the experimental corpus in the present study. This corpus has been annotated for part-of-speech (POS) information. Over half of it has been annotated for skeletal syntactic structure [43].

The top 10,000 most frequently used words were used to build the vocabulary, and the remaining words were treated as unknown and mapped to the <unk> token. Because the original Penn Treebank tag set does not contain some of the symbols used in this paper (e.g., Number sign, Dollar sign, Percent sign, and Ampersand), these symbols are added to the symbol tag.

5.2. Methodology

All of the parameters of the model were trained using the training set. The performance of the model was evaluated using the standard (per-word) perplexity measure in the test set.

Experiments were conducted on a PC with Intel Core i7, 32 GB of RAM, and a NVIDIAGTX1080Ti GPU running Ubuntu 18.04.3 LTS. Networks were constructed using tensorflow-gpu-1.10.0 with NVIDIA CUDA 9.0 and the NVIDIA CuDNN 7.1 library. In order to create superpositions of states, unitary operator and mixed state, We used: Quantum Toolbox in Python(QuTiP) [44].

5.3. Optimization

The models are trained by backpropagation through time. We backpropagate for 35 time steps using stochastic gradient descent with a fixed momentum of 0.9, where the learning rate is initially set to 1.0 and is halved if the perplexity does not decrease by more than 1.0 on the validation set after an epoch. The network is trained using mini-batches of size 128. The training process starts from the initial weights and learning rates, and it continues until there is no further improvement in accuracy on the training set; then, the learning rate is decreased by a factor of 10. This procedure is repeated once, so the final learning rate is one percent of the initial value. The parameters of the model are randomly initialized over a uniform distribution with support [0.05, 0.05]. As a regulariser, dropout with probability 0.5 is applied to the outputs of all layers except the last mlpconv layer. All of the networks used in the experiment section use GAP instead of fully connected layers at the top of the network, and the resulting vector is fed directly into the softmax layer.

5.4. Results

The hyperparameters of the model is summarized in Table 1. The networks we used in the experiment consist of three stacked mlpconv layers, and the mlpconv layers are followed by a spatial max pooling layer that down-samples the inputs.

d 70
mlpconv wconv1 5
w wconv1 5
wconv1 3
s 192
h 2
i 192
o 192
l 10
f Relu

Notes. CNN = convolutional neural network; MLP = multi-layer perceptron.

Table 1

Hyperparameter of the character-level CNN language model. Here, d represents the dimensionality of the character embeddings, w is the filter size and w=filter heights=filter widths. Additionally, s is the number of filters in each size, h is the number of MLP layers per mlpconv layer and i and o are the number of neurons in each of the two MLP layers. Here, l represents the number of neurons in the last MLP layer, and f represents nonlinearity functions.

Table 2 shows the comparison results of our model with states of the arts. Comparing with other models, the PPL of our model is slightly higher than LSTM-Char-Large and LSTM-2 [5,23]. However, the number of parameters in our model is around 6 million, which is significantly less than LSTM-Char-Large and LSTM-2. For the model with smaller size of parameters (e.g., KN-5), its PPL is 78% higher than our model. The main reasons are: (1) our QLM-based model is able to embedding not only a single word, but a sentence. Therefore, our model does not need additional filters to abstract the concept, and hence significantly reduces the number of parameters. (2) we add a NIN architecture to directly output the spatial average of the feature maps from the last mlpconv layer as the confidence of categories via a GAP layer. The resulting vector is fed into the softmax layer before final output.

Model PPL Size
CNN-MLPconv 79.1 6 m
LSTM-Char-Small 92.3 5 m
LSTM-Char-Large 78.9 19 m
KN-5 141.2 2 m
RNN 124.7 6 m
RNN-LDA 113.7 7 m
genCNN 116.4 8 m
FOFE-FNNLM 108.0 6 m
DeepRNN 107.5 6 m
Sum-Prod Net 100.0 5 m
LSTM-1 82.7 20 m
LSTM-2 78.4 52 m

Notes. CNN = convolutional neural network; PTB = Penn Treebank.

Table 2:

Comparison between the model proposed and other language models in terms of their performance on the English-language PTB test set. PPL stands for the perplexity and size refers to the approximate number of parameters in the model [5].

5.5. Discussion

5.5.1. Quantum semantic coding analysis

Currently, CNNs in NLP generally use word vector encoding, and the data generated have their own fixed internal order, such as a matrix that represents a sentence, with each row of the matrix representing a word [14,15]. Even in the latest character-level study [5], texts are stitched together in the order of the words. Given that approach, the convolution window should have the same width as the input matrix. In the present study, density operators are used as the CNN input, and the matrix is no longer a sequence of words but a representation of an uncertain state. At the same time, this approach solves the problem of an indefinite text length. To analyze whether it is better to use image-processing methods to process the density-operator text representation, we present the following two comparative experiments for discussion.

  • Comparison Experiment 1: Use the density operator as the CNN input, set the convolution window width to be the same as the width of the input, and use only one pair of convolution and pooling layers [5].

  • Comparison Experiment 2: Use word embedding as the CNN input, and the convolution operation is the same as in Section 4.2.

According to the results shown in Table 3, the following conclusions and speculations can be drawn:

  1. Combining density-operator representation with CNN-NIN could achieve significantly better results;

  2. When using word vectors as the input, the CNN-NIN structure did not bring significant improvements to the language model; and

  3. When using density-operator representation as the input, the image processing setting worked better for the CNN filters, that is, when using a filter width that differs from the input matrix's width.

Model PPL
Density Operator+CNN-non-static[5] 86.3
Word Vectors[5]+CNN–NIN 99.5
Density Operator+CNN–NIN 79.1

Notes. CNN = convolutional neural network; NIN = network-in-network; PTB = Penn Treebank.

Table 3:

The PPL results of the proposed model and the two comparative experiments on PTB. The model used in the first comparative experiment was a CNN that used a density-operator input and filters of the same width as the input. The model in the second comparative experiment used word-embedding input and CNN–NIN.

5.5.2. Effects of the number of mlpconv and MLP layers on the model

In this paper, ablation studies were applied to quantitatively analyze the role of the NIN network layer. We trained different models based on the settings listed in Table 4, and the results showed that the models that did not use NIN performed significantly worse. We speculated that the NIN network structure was a good fit for optimizing the CNN that used density-operator inputs. It derived more abstract concepts from the density operator through the non-linear structure of the MLP and enhanced the models generalization ability. Additionally, we trained another model that used the same number of layers as that of the NIN, solely to verify whether the performance decline was due to decrease in model size that was caused by not using the NIN. The results showed that this model performed significantly worse than the NIN network did.

The NIN network structure used significantly fewer parameters while achieving good performance; thus, it provided room for using more network layers. Therefore, we trained two models with more layers:

  • 10 layers of mlpconv, and each mlpconv layer had two layers of MLP, and

  • 3 layers of mlpconv, and each mlpconv layer had 10 layers of MLP.

The comparison results are shown in Table 4. Having more mlpconv or MLP layers did not lead to significant changes in the model.

WithoutNIN 10NIN+2MLP 3NIN+10MLP
filter - conv1–3 conv4–8 conv9–10 conv1 conv2 conv3
filtersize 3, 4, 5 8 5 3 8 5 3
filters 100, 100, 100 92 192 192 92 192 192
mlp layers - 2 2 2 10 10 10
nodes - 192 92 92(10) 192 92 92(10)
PPL 98.1 78.9 79.5

Notes. MLP = multi-layer perceptron; NIN = network-in-network.

Table 4:

Effects of layer settings of the NIN, mlpconv and MLP on the model.

6. CONCLUSION

This article presents a new NLM whose input is a character-level density operator. This model has fewer parameters but performs better than do baseline models that use word or character embeddings. Analyzing the experimental results shows that the quantum semantic space model can extract rich semantic and orthographic features. Using a CNN in the NIN is an effective method of representation learning. At present, most studies on NLP use words as input and must consider the word order. Even if character-level input is used, word-level analysis is still required after feature learning. In the present study, the input texts are first coded at the character level and then represented using the quantum semantic space model, and the density operator represents an uncertain state of the basic constituent units (characters). Therefore, a long text is represented by a mixed state and hence it can be integrated into a neural network. Using more concepts (such as entanglement) of quantum theory for text representation will be our next research step, as will finding more applications of this model for NLP tasks such as prediction or machine translation.

CONFLICT OF INTEREST

Authors have no conflict of interest to declare.

ACKNOWLEDGMENTS

This work was jointly supported by the Social Science Project of Shandong Province (Nos. 18CSPJ03, 18CHLJ09, 16CFXJ05), the National Natural Science Foundation of China (NSFC, Project No. 71801142), the Industry-University Cooperation and Education Project of Ministry of Education of China (201802047030), the Humanities and Social Sciences Research Project of Ministry of Education of China (17YJC630077).

REFERENCES

1.Y. Bengio, R. Ducharme, P. Vincent, and C. Jauvin, A neural probabilistic language model, J. Mach. Learn. Res., Vol. 3, 2003, pp. 1137-1155.
2.A. Mnih and G.E. Hinton, A scalable hierarchical distributed language model, in Advances in Neural Information Processing Systems, 2009, pp. 1081-1088.
3.C.D. Santos and B. Zadrozny, Learning character-level representations for part-of-speech tagging, in Proceedings of the 31st International Conference on Machine Learning (ICML-14) (Beijing), 2014, pp. 1818-1826.
4.X. Zhang, J. Zhao, and Y. LeCun, Character-level convolutional networks for text classification, in Advances in Neural Information Processing Systems, 2015, pp. 649-657.
5.Y. Kim, Y. Jernite, D. Sontag, and A.M. Rush, Character-aware neural language models, in Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16), 2016, pp. 2741-2749.
6.J. Macalister, Speed reading courses and their effect on reading authentic texts: a preliminary investigation, Reading Foreign Lang., Vol. 22, 2010, pp. 104.
8.A. Sordoni and J.Y. Nie, Looking at vector space and language models for IR using density matrices, in International Symposium on Quantum Interaction (Leicester), 2013.
9.P. Zhang, J. Niu, Z. Su, B. Wang, L. Ma, and D. Song, End-to-end quantum-like language models with application to question answering, in The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18), 2018, pp. 5666-5673.
12.W.-C. Cheng, S. Kok, H.V. Pham, H.L. Chieu, and K.M.A. Chai, Language modeling with sum-product networks, in Fifteenth Annual Conference of the International Speech Communication Association, 2014.
13.M. Wang, Z. Lu, H. Li, W. Jiang, and Q. Liu, $ gen $ CNN: a convolutional architecture for word sequence prediction, 2015. arXiv preprint arXiv:1503.05034
14.Y. Kim, Convolutional neural networks for sentence classification, 2014. arXiv preprint arXiv:1408.5882
15.Y. Zhang and B. Wallace, A sensitivity analysis of (and practitioners’ guide to) convolutional neural networks for sentence classification, in Proceedings of the Eighth International Joint Conference on Natural Language Processing (Volume 1: Long Papers) (Taipei), Vol. 1, 2017, pp. 253-263.
16.A. Pauls and D. Klein, Faster and smaller n-gram language models, Association for Computational Linguistics, in Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies (Portland), Vol. 1, 2011, pp. 258-267.
17.M. Penagarikano, A. Varona, L.J. Rodriguez-Fuentes, and G. Bordel, Dimensionality reduction for using high-order n-grams in SVM-based phonotactic language recognition, in Twelfth Annual Conference of the International Speech Communication Association (Prague), 2011.
20.T. Luong, R. Socher, and C. Manning, Better word representations with recursive neural networks for morphology, in Proceedings of the Seventeenth Conference on Computational Natural Language Learning (Sofia), 2013, pp. 104-113.
21.J. Botha and P. Blunsom, Compositional morphology for word representations and language modelling, in International Conference on Machine Learning (Beijing), 2014, pp. 1899-1907.
22.S. Qiu, Q. Cui, J. Bian, B. Gao, and T.-Y. Liu, Co-learning of word representations and morpheme representations, in Proceedings of COLING 2014, the 25th International Conference on Computational Linguistics: Technical Papers (Dublin), 2014, pp. 141-150.
23.W. Zaremba, I. Sutskever, and O. Vinyals, Recurrent neural network regularization, 2014. arXiv preprint arXiv:1409.2329
24.A. Graves, Generating sequences with recurrent neural networks, 2013. arXiv preprint arXiv:1308.0850
27.Y. Xiao and K. Cho, Efficient character-level document classification by combining convolution and recurrent layers, 2016. arXiv preprint arXiv:1602.00367
29.P.D. Bruza and R.J. Cole, Quantum logic of semantic space: an exploratory investigation of context effects in practical reasoning, 2006. arXiv preprint quant-ph/0612178
32.E. Grefenstette, M. Sadrzadeh, S. Clark, B. Coecke, and S. Pulman, Concrete sentence spaces for compositional distributional models of meaning, in Proceedings of Computational Semantics (IWCS 2011), 2011, pp. 125.
33.W. Blacoe, E. Kashefi, and M. Lapata, A quantum-theoretic approach to distributional semantics, in Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Atlanta), 2013, pp. 847-857.
35.M. Lin, Q. Chen, and S. Yan, Network in network, 2013. arXiv preprint arXiv:1312.4400
37.J.C.H. Chen, Quantum computation and natural language processing, 2002.
39.T. Mikolov, I. Sutskever, A. Deoras, H.-S. Le, S. Kombrink, and J. Cernocky, Subword language modeling with neural networks, 2012. http://www.fit.vutbr.cz/imikolov/rnnlm/char.pdf
42.R. Pascanu, C. Gulcehre, K. Cho, and Y. Bengio, How to construct deep recurrent neural networks, 2013. arXiv preprint arXiv:1312.6026
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
12 - 2
Pages
1613 - 1621
Publication Date
2019/11/25
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.2991/ijcis.d.191114.001How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Zhihao Wang
AU  - Min Ren
AU  - Xiaoyan Tian
AU  - Xia Liang
PY  - 2019
DA  - 2019/11/25
TI  - Character-Level Quantum Mechanical Approach for a Neural Language Model
JO  - International Journal of Computational Intelligence Systems
SP  - 1613
EP  - 1621
VL  - 12
IS  - 2
SN  - 1875-6883
UR  - https://doi.org/10.2991/ijcis.d.191114.001
DO  - 10.2991/ijcis.d.191114.001
ID  - Wang2019
ER  -