Rigorous Analysis of Multi-Factorial Evolutionary Algorithm as Multi-Population Evolution Model
- DOI
- 10.2991/ijcis.d.191004.001How to use a DOI?
- Keywords
- Multi-factorial evolutionary algorithm; Multi-population evolution model; Multi-task optimization; Knowledge transfer; Across-population
- Abstract
Multi-task optimization algorithm is an emergent paradigm which solves multiple self-contained tasks simultaneously. It is thought that multi-factorial evolutionary algorithm (MFEA) can be seen as a novel multi-population algorithm, wherein each population is represented independently and evolved for the selected task only. However, the theoretical and experimental evidence to this conclusion is not very convincing and especially, the coincidence relation between MFEA and multi-population evolution model is ambiguous and inaccurate. This paper aims to make an in-depth analysis of this relationship, and to provide more theoretical and experimental evidence to support the idea. In this paper, we clarify several key issues unsettled to date, and design a novel across-population crossover approach to avoid population drift. Then MFEA and its variation are reviewed carefully in view of multi-population evolution model, and the coincidence relation between them are concluded. MFEA is completely recoded along with this idea and tested on 25 multi-task optimization problems. Experimental results illustrate its rationality and superiority. Furthermore, we analyze the contribution of each population to algorithm performance, which can help us design more efficient multi-population algorithm for multi-task optimization.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Evolutionary algorithms (EAs) inspired by Darwinian's principle of “natural selection or survival of the fittest,” are a class of genetic population-based metaheuristics [1]. Through computational analogues of sexual reproduction or mutation, they are capable of producing the offspring who can survive to the next generation and likely move together towards fitter regions of the search landscape. Over the past decades, EAs have been successfully applied to solve a wide variety of complex optimization problems in science and engineering. These problems can essentially be divided into two main categories: single-objective optimization and multi-objective optimization [2].
Multi-task optimization (MTO) is an emergent paradigm in evolutionary computation, that focuses on dealing with multiple self-contained tasks simultaneously using a single run of EA [3]. Note that it is classified into one of three distinct conceptual realizations developed for transfer optimization [4]. Part of the original motivation behind the idea came from the observation that real-world problems seldom exist in isolation and every human being possesses the most remarkable ability to effectively manage and execute multiple tasks at the same time, for example, talking while walking or driving [5]. Inspired by the well-established model of multi-factorial inheritance, multi-factorial evolutionary algorithm (MFEA) was recently proposed to efficiently realize the MTO paradigm [6]. If the optimization tasks happen to bear some commonality or complementarity, then the inclusion of knowledge transfer often leads to significant performance improvements relative to conventional EAs alone.
In past decades, many multi-population techniques were developed to improve the optimization performance of EAs and swarm intelligence algorithms [7]. The original population is divided into multiple small homogeneous or heterogeneous populations to tackle various optimization problems. Existing results demonstrate that multi-population method is able to search different spaces simultaneously, and in favor of population diversity. Note that the concept of multi-population is also described using other terms such as multi-swarm, parallel, cooperative, co-evolution, island, and so on.
A key cornerstone of MFEA is the unified representation scheme of solutions in a uniform search space. All individuals have the chance to evolve through a common law. On the other hand, each individual in a population has its own task, which means that the whole population can be viewed as being divided into multiple populations by task assignment. Thus, MFEA can be naturally explained as a special multi-population evolution model and some features, which are different from the standard island model, were also outlined in [8]. However, the evidence for this conclusion is not abundant enough, although it seems like that this conclusion is widely accepted. For example, in algorithm analysis, the coincidence relation between MFEA and multi-population evolution model is not clear. Furthermore, there is no experimental verification to support this conclusion.
In this paper, four key questions are answered firstly to clear up any misunderstandings, including performance evaluation, evaluation numbers, population drift, and population size. In view of multi-population evolution model, the algorithm details of MFEA are explained carefully and then the coincidence relation between them are concluded. Furthermore, other MTO paradigms currently proposed are also reviewed by a similar measure. These analysis results indicate a way to design efficient MTO algorithms with novel evolutionary operators. Next, the basic structure of MFEA is reframed following multi-population evolution model, and some key operators and parameters are redefined in order to ensure the consistency with the original MFEA. Experimental results demonstrate its rationality. What's more, with the help of new multi-population MFEA, we can analyze the evolution process precisely and then design more efficient multi-population EA algorithm for MTO.
Within this context, the contribution to evolutionary computation of this paper is some solid evidence to support, both theoretically and experimentally, that MFEA can be explained and executed as multi-population evolution model. More specifically, the innovative work contains threefold. First, the conventional MFEA is explained in view of multi-population evolution model, and the coincidence relation between them is also summarized. Second, following the same idea, other variations of MFEA are reviewed to indicate potential scheme of new operator in MTO paradigm. Third, experimental results on three test suites containing 25 MTO benchmark problems illustrate two versions (namely single-population and multi-population) of MFEA have equal efficacy, and multi-population evolution model facilitates designing more efficient EAs for MTO.
The rest of this paper is organized as follow. Section 2 describes the related background, including single-population evolution model, multi-population evolution model, detailed description of MFEA, and related works on MTO. In Section 3, we first answer some key issues, which are very confused and not solved by Hashimoto [8] or other researchers. Then MFEA and its variation are reviewed carefully in view of multi-population evolution model. The basic structure of multi-population MFEA is proposed in Section 4, and then two MFEA algorithms are compared in order to reveal our work's rationality and superiority. Finally, the work in this paper is concluded and the future works are discussed in Section 5.
2. BACKGROUND
2.1. Single-Population Evolution Model
The canonical EA model is run based on one population, as shown in Figure 1. The evolution model starts from an initial population of individuals (solutions) generated randomly. Then it incorporates standard steps of offspring reproduction (through genetic operators like crossover and mutation) followed by a computational analogue of natural selection. As a result, it can gradually guide an evolving population towards favorable regions, which are characterized by high fitness values in the search space [9].

Single-population evolution model for a single task.
2.2. Multi-Population Evolution Model for MTO
For MTO, multiple tasks should be well approached at the same time. Solving this optimization in a natural way is the multi-population evolution strategy, which allows each subpopulation to exploit separate search space in order to solve the corresponding task. As an example, in Figure 2, a multi-population evolution model is depicted to solve two tasks.
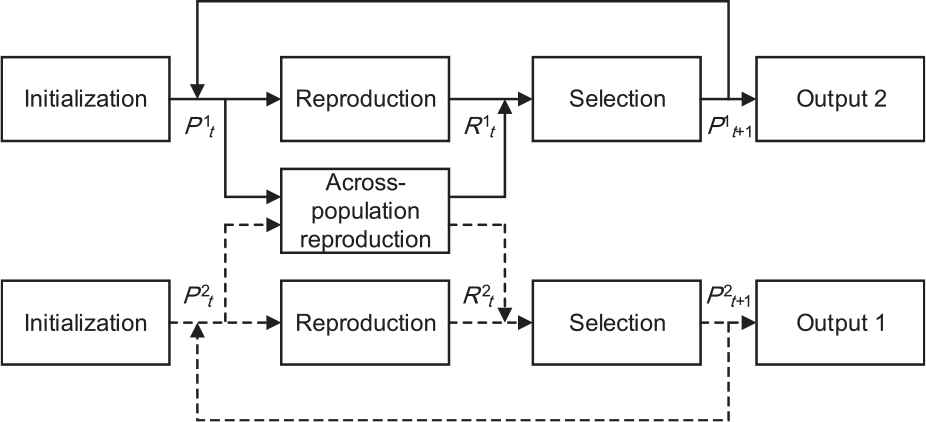
Multi-population evolution model for a simple case comprising two tasks.
In multi-population evolution model, two subpopulations evolve independently according to different (or same) evolutionary schemes, and then export their best solutions as the final solution of each task. Compared with Figure 1, a core feature of multi-population evolution model is the across-population reproduction operator, which is deemed to help exchange information and assist to find the promising solutions.
Another important feature is that the parent and its child individual must belong to and evolve in the same subpopulation. One of the advantages of it is to maintain population stability as far as possible. To depict this feature in Figure 2, solid line and dotted line represent different evolution process of two subpopulations. Of course, the child individual (R1t) in subpopulation 1 may be produced with the help of the individuals (P2t) from subpopulation 2, and vice versa.
2.3. Multi-Factorial Evolutionary Algorithm
As the first implementation, MFEA corporates genetic algorithm (GA) into the MTO paradigm [6]. To efficiently tackle the across-task knowledge, the feasible solutions are encoded into a unified search space Y by the uniform random-key scheme [10]. Generally, if there are K tasks to be optimized, Y is normalized to [0, 1]D, where the dimension number D should be max{Dj} and j = 1, 2, …, K. To compare the individuals for multi-tasking optimization, the following properties are assigned to each individual.
Factorial Cost: In general, the factorial cost fji of individual pi is its fitness value on a particular task Tj.
Factorial Rank: The factorial rank rji is simply defined as the index of pi in the list of population members sorted in ascending order with respect to their factorial cost on specific task Tj.
Scalar Fitness: The scalar fitness of
Skill Factor: The skill factor
The basic structure of MFEA is shown in Algorithm 1 [6]. Similar to other classical EAs, it also stars with a randomly generated population (line 1), and all individuals are evaluated on all tasks (line 2). All individuals are distributed across this space, and each individual is assigned a skill factor in population initialization (line 3).
Algorithm 1: Multi-factorial Evolutionary Algorithm.
Input: K tasks (T1, T2, … , TK)
Parameter: random mating probability (rmp)
Output: K best solutions (S1, S2, … , SK)
1: Generate an initial population randomly and store it in current-pop
2: Evaluate every individuals with respect to every optimization task in multi-tasking environment
3: Compute the skill factor of each individual
4: while stopping conditions are not satisfied do
5: Apply genetic operators on current-pop to generate an offspring-pop
6: Evaluate the individuals in offspring-pop for selected optimization task only
7: Concatenate offspring-pop and current-pop to form an intermediate-pop
8: Update the scalar fitness and skill factor of every individual in intermediate-pop
9: Select the fittest individuals from intermediate-pop to form the next current-pop
10: end while
During evolution (lines 4–10), MFEA uses assortative mating and vertical cultural transmission firstly to generate the offspring (line 5), thereby leading to population diversification and implicit knowledge transfer across different tasks.
Assortative mating: For the two randomly selected parents pa and pb, if they possess the same skill factor
Vertical cultural transmission: For a given offspring c generated by assortative mating, if it is generated by the crossover of two parents pa and pb, its skill factor
At the end of each iteration, MFEA adopts an elitist selection strategy (lines 6–9) that ensures that the fittest individuals will survive through the generations.
2.4. Related Works on MTO
Since the first invention of MFEA in 2016, intensive research efforts have been devoted to this area. For the sake of clarity, these works can be divided into three categories: algorithm framework, algorithm improvement, and typical application [11]. Several ways of algorithm improvement will be discussed in Section 3.3, and influential results in terms of algorithm framework and typical application are mentioned here to reflect the latest progress of the discipline.
A general framework, the evolution of biocoenosis through symbiosis (EBS), was proposed for EAs to deal with many-tasking problems [12]. This framework has two main features, i.e., the adaptive control of knowledge transfer among tasks and the selection of candidates for evaluation from concatenate offspring. Another multi-population evolution framework (MPEF) was first established for MTO, wherein each population addresses its own optimization task and genetic material transfer can be implemented and controlled in an effective manner [13]. A multi-task bi-level evolutionary algorithm (M-BLEA) was provided as a promising paradigm to enhance the performance of bi-level optimization [14]. In M-BLEA, lower level optimization is a multi-task problem, which can speed up the convergence to high quality solutions and also promote solving the upper level problem. Recently, MTO with dynamic resource allocation (MTO-DRA) was proposed [15]. It can allocate and control computational resources to each task adaptively according to the requirements.
In the literature, there exist a lot of works to apply MFEA to tackle real-world problems, such as complex supply chain network management [16], bi-level optimization problem [14], double-pole balancing problem [17], composites manufacturing problem [14,18], branch testing in software engineering [19], cloud computing service composition problem [20], pollution-routing problem [21], operational indices optimization of beneficiation process [22], and time series prediction problem [23].
3. ANALYSIS OF MFEA AND ITS VARIANTS IN TERMS OF MULTI-POPULATION EVOLUTION MODEL
As the most famous MTO paradigm, MFEA has wide applications in complex scientific and engineering optimization problems, and lays an important basis for later progress in evolutionary computation area [24]. Thus, a deep analysis of it can help us to understand other existing MTO paradigms and design novel ones in terms of multi-population evolution model.
Notice that, more theoretical and experimental evidence are provided in this paper to support the idea that the canonical MFEA can be explained and executed as multi-population evolution model. Thus, MFEA and its variants are analyzed carefully, but we don't try to improve or modify MFEA in any way in this section.
3.1. Key Issues to be Settled
In MFEA, each individual in a population has its own task and the task assignment is based on its relative strength (skill factor) for each task [8]. As a result, a population can be viewed as being divided into multiple subpopulations by the task assignment. In other word, individuals with the same skill factor can be regarded as a subpopulation. The number of subpopulations is the same as that of tasks to be solved. Under this assumption and consensus, four specious questions are explained firstly as following.
Question 1: How to properly evaluate the individual's performance?
In evolutionary computation theory, direct fitness is a good measure of an individual's ability to survive and reproduce. In contrast, an individual's performance is evaluated by the scalar fitness in MFEA, not the objective function value as usual. The scalar fitness is calculated based on factorial rank, and the factorial rank further comes from factorial cost, which is equal to the objective function value. Clearly, the intention of these concepts is that it is possible to thoroughly evaluate an individual for all optimization tasks.
However, an interesting observation from algorithm implementation is, in order to reduce the total number of function evaluations as many as possible, an individual generated in MFEA is evaluated by objective function on one valid task only [6]. This means that the scalar fitness and the objective function value are in one-to-one correspondence. In short, the objective function value is an ideal alternative of the scalar fitness in algorithm implementation.
Question 2: How to reduce the potentially large number of function evaluations per iteration?
In multi-population evolution model, in view of each individual assigned in one subpopulation, it is evaluated only once in its search space. In theory, each individual in a uniform search space must be evaluated for all tasks, and then it is assigned to one subpopulation based on its skill factor. However, it requires a prohibitively large number of function evaluations to achieve a good result.
In the actual implementation process, instead of evaluating an offspring for every task, the offspring is evaluated only for one task that is its parent's skill factor. As mentioned above, the incorporation of cultural effects can significantly reduce the total number of function evaluations required as noted in [6].
Question 3: How to avoid population drift during across-population crossover?
In MFEA, by vertical cultural transmission, the algorithm allows the offspring to imitate the skill factor of any one of their parents. When the offspring undergoes across-population crossover, it has half chance to drift to other subpopulation, and the parent and his child may be attached to the different subpopulations. This result doesn't coincide with the basic feature of multi-population evolution model.
In order to avoid population drift, a new simulated binary crossover (SBX) approach across subpopulations Pk and Pr (k ≠ r) is proposed as follows:
Question 4: How to control the population size during population evolution?
General speaking, for multi-population evolution, a fixed size of each subpopulation is given in the initialization stage. Based on the definition of skill factor in MFEA, the subpopulation size depends on the skill factor of individuals and varies over population evolution period. The more the number of individuals with the same skill factor, the larger its subpopulation size.
It is seemingly a contradiction. In fact, if the algorithm strictly follows the original intention, we will get out of control MFEA algorithm. Therefore, in order to avoid it happening, in the population iteration process, the number of the fittest individuals is fixed to form the next subpopulation [6]. That is to say, the subpopulation size is equal to the total population number divided by the number of tasks to be solved.
3.2. Micro-Level Analysis of MFEA
After answering these key and easily confused questions, now we can reexamine MFEA operators in view of multi-population evolution model as follows.
Population initialization (lines 1–3 in Algorithm 1) is understood lightly as a multi-population approach and omitted here for simplicity. Population iteration (lines 4–10 in Algorithm 1) is the focus of our research in this section. We start from the current-pop
Initially, assortative mating (line 5 in Algorithm 1) is applied on current-pop to generate an offspring-pop. According to the definition of assortative mating in MFEA, two parent candidates (pa and pb) selected randomly from current-pop may undergo one of three genetic operators as follows. First, two individuals from the same task will crossover and mutate as single-population reproduction in Figure 2. Second, two individuals from two different tasks may crossover and mutate as across-population reproduction in Figure 2. Lastly, two individuals from two different tasks may only mutate independently of each other as other single-population reproduction in Figure 2.
After that, vertical cultural transmission is run in MFEA. One of the following three operations will happen corresponding to the above three cases. For the first and third cases, two offspring individuals belong to their parent populations evidently, which are unique and definite. However, the second case becomes complicated. At this time, it is possible that the offspring individuals belong to the opposing parent subpopulation, which means this result does not coincide with multi-population evolution model. Fortunately, this inconsistency can be prevented simply, as explained in Section 3.1, by novel crossover operator described in Eq. (1). As a result, the child and his parent individuals are in the same subpopulation.
After reproduction (crossover and mutation), two subpopulations (
The next step is to update the scalar fitness and skill factor (line 8 in Algorithm 1). As mentioned above, all individuals are only evaluated on a special task only (the fitness value is infinite for other tasks), which means the skill factor does not change from one task/subpopulation to another. Therefore, this step can be skipped for multi-population evolution model.
The last iterative step is to select the fittest individuals to form the next current-pop
In a word, the conventional MFEA can be explained reasonably in terms of multi-population evolution model, even though it is originally designed as single-population EA strategy. Accordingly, it is essential to indicate explicitly the comparison relationship of each element, operator, and parameter between MFEA and multi-population evolution model, as listed in Table 1.
| MFEA | Multi-Population Evolution Model |
|---|---|
| Population (Pt) | Subpopulations |
| Random-key representation in a unified search space | Direct representation in single search space |
| Across-domain decoding | None |
| Scalar fitness, factorial rank, factorial cost | Function fitness |
| Single-population SBX | Eq. (12) |
| Across-population SBX | Eq. (1) |
| Polynomial mutation | Polynomial mutation |
| Elitist selection strategy | Elitist selection strategy |
| Random mating probability (rmp) | Across-population reproduction probability (arp) |
The comparison relationship between MFEA and multi-population evolution model.
3.3. Other Works Analysis
To make multi-population method more efficient, several basic issues of the algorithm design should be solved, including the number of subpopulations, the communication between subpopulations, the search area of each subpopulation, and the search strategy of each subpopulation [7]. Considering the particularity of MTO, the number of subpopulations is fixed as the number of tasks, and the search area is a unified search space for each subpopulation in general. Therefore, in order to plan a new multi-population EA for MTO as shown in Figure 2, it is crucial to design the reproduction operator (including single-population reproduction, across-population reproduction, occurrence intensity of knowledge transfer, etc.) and selection operator (including evaluation method, comparison level, selection strategy, etc.), respectively. Each new operator, in a sense, often leads to a novel EA for MTO. The purpose of this section is twofold. We argue that (1) other variants of MFEA can also be explained as multi-population evolution model; and (2) these existing operators facilitate and inspire more innovative and efficient operator, or even algorithm.
Although not clearly stated, up to now, several interesting approaches were proposed to follow along with multi-population evolution model.
(1) Single-population reproduction. It is the same as the normal reproduction in single-population evolution model shown in Figure 1. As a core search operator, it can significantly affect the performance of multi-population EAs, and be used to distinguish them.
The most widely utilized one is probably genetic mechanisms, namely crossover and mutation. Specifically, several typical genetic strategies include SBX [6,17], ordered crossover [25], one-point crossover [26], guided differential evolutionary crossover [27], Gaussian mutation [6], swap mutation [25], polynomial mutation [17,28], and swap-change mutation [29]. The other three EAs, differential evolution (DE) [13,30–32], particle swarm optimization (PSO) [31,33–35], and genetic programming (GP) [23], are also utilized as fundamental algorithm for MTO paradigms.
(2) Across-population reproduction. The prominent difference between Figures 1 and 2 is across-population reproduction operator in MPEF. Its major function is knowledge transfer between different subpopulations, which may help accelerate the search process and find global solutions. The most natural and direct way is a similar operation as single-population reproduction.
Take MFEA as an example, knowledge transfer is done by across-population SBX crossover as below [6]:
Compared with single-population SBX crossover, two parents come from two different subpopulations (Pk and Pr). For MT-CPSO (multi-tasking coevolutionary PSO), the across-population reproduction is provided as follows [33]:
In addition to these routine operations, another interesting reproduction approach is called explicit genetic transfer across tasks and proposed recently [36]. By configuring the input and output layers to represent two task domains, the hidden representation provides a possibility for conducting knowledge transfer across task domains. In particular, let P and Q represent the set of solutions uniformly and independently sampled from the search space of two different tasks T1 and T2, respectively. Then the mapping M from T1 to T2 is given by
Therefore, the transfer of useful genetic solutions can be conducted simply by multiplication operation with the learned M. It is very recently that a novel genetic transform strategy has been proposed [37]. Given two tasks T1 and T2, two mapping vectors M12 (from T1 to T2) and M21 (from T2 to T1) are calculated as follows:
In many-task optimization environment, a task may be only helpful to some tasks. Therefore, it is important to choose the most suitable task (or assisted task) to be paired with the present task (or target task) for knowledge transfer. An adaptive selection mechanism of choosing suitable task was proposed by simultaneously considering the similarity between tasks and the accumulated rewards of knowledge transfer during the evolution [38].
(3) Occurrence intensity of knowledge transfer. As illustrated in Figure 2, the offspring can be generated in two ways: single-population reproduction and across-population reproduction. On one hand, some inductive biases provided by another task/subpopulation are helpful to improve performance. On the other hand, excessive across-population reproduction may lead to negative genetic transfer and bad algorithm performance [5]. Thus a natural question in multi-population evolution model is how to adjust the intensity of knowledge transfer.
In classic MFEA, parameter rmp is used to balance the diversity and convergence capability of obtained solutions and is set as a constant of 0.3 [6]. A larger value of rmp induces more exploration of the entire search space, thereby facilitating population diversity. In contrast, a smaller value would encourage the exploitation of current solutions and speed up the population convergence. In TMO-MFEA, a larger rmp is used for diversity-related variables to enhance its diversity, while a smaller rmp is designed for convergence-related variables to achieve a better convergence [22,39].
In fact, knowledge transfer across tasks can also occur with a fixed generation interval along the evolution search. In EMT (evolutionary multi-tasking), the interval of across-population reproduction is set to 10 generations [36]. Experimental results based on island model reveal that better results are observed from small transfer intervals than large transfer intervals [8].
In MT-CPSO, if a particle does not improve its personal best position over a prescribed consecutive generation, the across-population reproduction operator is then triggered [33]. Obviously, the greater the value of the prescribed iterations, the smaller the probability of across-population reproduction.
Another potential research direction is parameter control or adaptation, especially for rmp. If a task can be improved more times by the offspring from other tasks, the probability of knowledge transfer should be increased; otherwise, we will decrease this rate [12]. Thus the probability is defined by
(4) Evaluation method. General speaking, the complete definition of a good selection operator is composed of evaluation, comparison, and selection method. The individual's performance can be evaluated directly or indirectly. As an indirect method, the scalar fitness was originally proposed in MFEA [6]. On the other hand, the fitness value of objective function is a nature and typical direct method [12,13,32,33]. As indicated in Section 3.1, scalar fitness and function fitness are equivalence relation in multi-population evolution model.
(5) Comparison level. After evaluating all individual's performance (function fitness or scalar fitness), the next question is the scope or level of comparison objects. In MFEA, the offspring-pop (Rt) and current-pop (Pt) are concatenated and then a sufficient number of individuals are selected to yield a new population [6]. This approach can be called population-based (or all-to-all) comparison. As a contrast, individual-based (or one-to-one) comparison is also utilized [13,23,30,33]. Once the off-spring individual is generated by single-population or across-population reproduction, it is compared with its parent directly and then the better one can remain in the next generation.
(6) Selection strategy. For the case of population-based comparison, some alternative strategies are proposed to select the fittest individuals from the joint population. For example, MFEA and its variation follow elitist selection [6], level-based selection [28], and self-adaptive selection [40]. Furthermore, it may remove the worse or redundant individuals so as to create more population diversity [23].
4. EXPERIMENTAL VERIFICATION AND DISCUSSION
4.1. Algorithm Implementation
In order to illustrate the rationality of multi-population evolution model, the most classic MTO paradigm is completely recoded as shown in Algorithm 2 and its flowchart is also depicted in Figure 3. In fact, two versions of MFEA were proposed by Gupta [6] and Da [41], respectively. They differ on (1) the relation between crossover and mutation, and (2) the mutation method performed. In consideration of rich experimental results and simple structure, MFEA proposed by Da in [41] is confirmed as the baseline algorithm in this paper.
Algorithm 2: Multi-population MFEA.
Input: K tasks (T1, T2, …, TK)
Parameter: across-population reproduction probability (arp)
Output: K best solutions (S1, S2, …, SK)
1: for each task Tk do
2: Generate an initial subpopulation Pk randomly
3: Evaluate all individuals in subpopulation Pk based on task Tk
4: Find the best solution Sk for task Tk
5: end for
6: while stopping conditions are not satisfied do
7: for each task Tk do
8: for each individual xik in subpopulation Pk do
9: if rand < 0.5 then
10: Select j-th individual xjk in subpopulation Pk randomly
11: Generate an offspring individual based on (12)
12: elseif rand < arp + 0.5 then
13: Select j-th individual xjr in subpopulation Pr randomly
14: Generate an offspring individual based on (1)
15: end if
16: Apply polynomial mutation on individual xik
17: Evaluate individual xik based on task Tk
18: end for
19: Concatenate the offspring subpopulation oPk and the current subpopulation Pk to form an intermediate subpopulation
20: Select the fittest individuals from intermediate subpopulation to form the next subpopulation Pk+ 1
21: Update the best solution Sk for task Tk
22: end for
23: end while
24: Return K best solutions (S1, S2, …, SK)
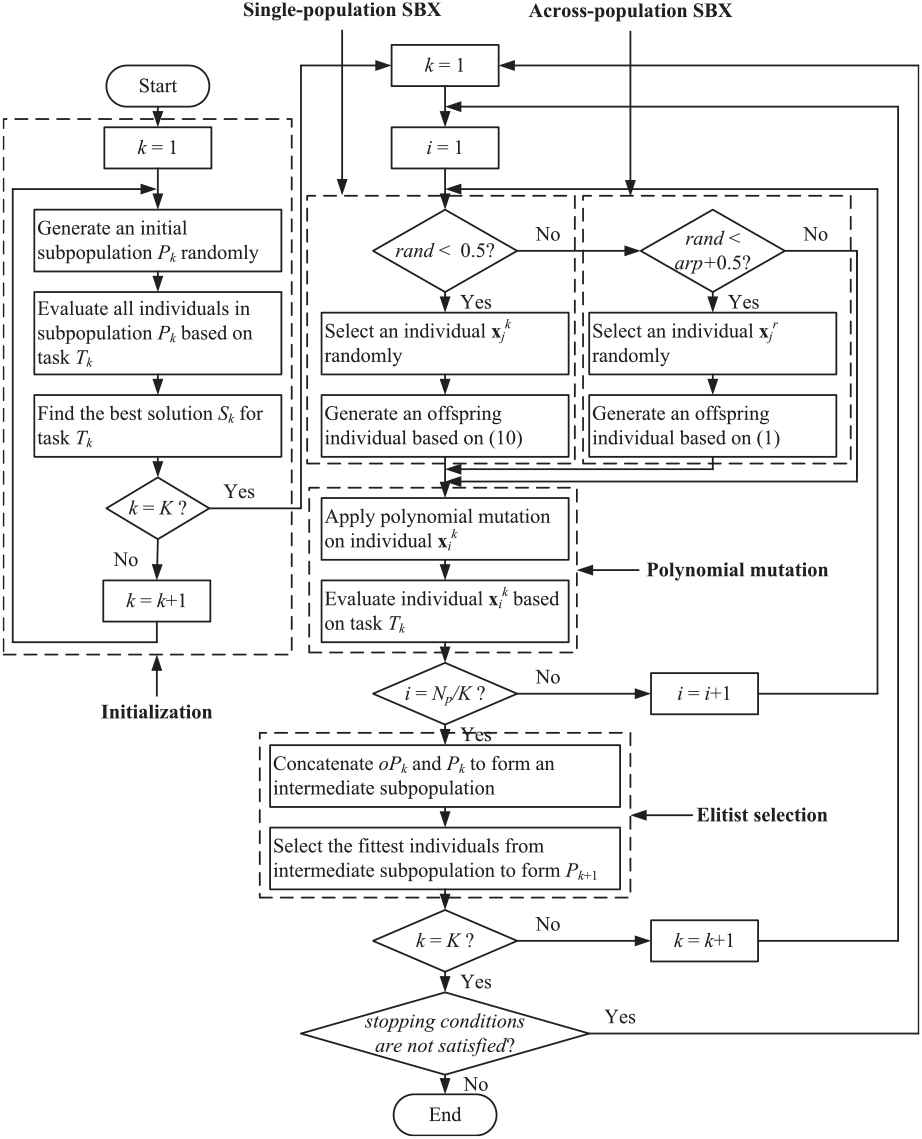
Flowchart of multi-population multi-factorial evolutionary algorithm.
In population initialization (lines 1–5 in Algorithm 2), K subpopulations (P1, P2, …, PK) are generated randomly and evaluated based on each task Tk (k = 1, 2, …, K). This process corresponds to lines 1–3 of Algorithm 1. Note that, as mentioned above, function fitness based on task Tk is the evaluation object for each individual in subpopulation Pk.
In population evolution (lines 6–23 in Algorithm 2), each individual
The second (lines 12–14 in Algorithm 2) is SBX across subpopulations (Pk and Pr) with a probability of arp as described by (1). The last way is to remain unchanged temporarily.
Similar to the single-population MFEA, in order to update each next subpopulation (Pk+ 1), multi-population MFEA also adopts an elitist selection strategy (lines 19–21 in Algorithm 2) according to the scalar fitness. Following that, we will update the best solution set for the current task Tk.
What needs to be pointed out is that no separate local search step is performed in Algorithm 2. In contrast, in MFEA proposed by Gupta, all individuals undergo a simple local search (quasi-newton algorithm) to improve solution quality [6]. Thus, it is the third difference between two MFEA versions in algorithm design and implementation.
4.2. Experimental Setup
Single-population MFEA proposed by Da in [41] is abbreviated as sp-MFEA in this section. To express conveniently, multi-population MFEA as shown in Algorithm 2 is abbreviated as mp-MFEA.
In this section, we present the details of MTO benchmark problems and parameter setting in our experiments.
4.2.1. Benchmark problems
Three test suites containing 25 MTO problems are employed in the experiment. These MTO problems possess different degrees of latent synergy between their involved component tasks.
The first benchmark suite contains nine standard single-objective MTO problems, which details can be referred to the technical report [41]. The second benchmark suite contains ten complex single-objective MTO problems, and each task is a benchmark function from 2014 IEEE Congress on Evolutionary Computation (CEC 2014). They are both provided by Feng et al. in the Competition on Evolutionary Multi-task Optimization, CEC 2019, and are available at
| Test Suite | MTO Problem | Base Functions |
|---|---|---|
| 1 | Griewank (T1), Rastrigin (T2) | |
| 2 | Ackley (T1), Rastrigin (T2) | |
| 3 | Ackley (T1), Schwefel (T2) | |
| 4 | Rastrigin (T1), Sphere (T2) | |
| Standard 2-tasks problem | 5 | Ackley (T1), Rosenbrock (T2) |
| 6 | Ackley (T1), Weierstrass (T2) | |
| 7 | Rosenbrock (T1), Rastrigin (T2) | |
| 8 | Griewank (T1), Weierstrass (T2) | |
| 9 | Rastrigin (T1), Schwefel (T2) | |
| 10 | #7 (T1), #8 (T2) | |
| 11 | #7 (T1), #12 (T2) | |
| 12 | #7 (T1), #15 (T2) | |
| 13 | #8 (T1), #15 (T2) | |
| Complex 2-tasks problem | 14 | #9 (T1), #10 (T2) |
| 15 | #9 (T1), #11 (T2) | |
| 16 | #10 (T1), #16 (T2) | |
| 17 | #11 (T1), #13 (T2) | |
| 18 | #13 (T1), #14 (T2) | |
| 19 | #14 (T1), #16 (T2) | |
| 20 | Griewank (T1), Rastrigin (T2), Ackley (T3) | |
| 21 | Ackley (T1), Rastrigin (T2), Weierstrass (T3) | |
| 22 | Rastrigin (T1), Sphere (T2), Rosenbrock (T3) | |
| 3-tasks problem | 23 | Ackley (T1), Rosenbrock (T2), Weierstrass (T3) |
| 24 | Rosenbrock (T1), Rastrigin (T2), Griewank (T3) | |
| 25 | Griewank (T1), Weierstrass (T2), Sphere (T3) |
MTO = multi-task optimization.
Description of 25 MTO problems.
4.2.2. Parameter setting
While rmp is utilized in MFEA, arp is utilized in Algorithm 2. Their values are set equal to 0.3 and 0.15, respectively. Figure 4 describes the role of these key parameters in two MFEA algorithms vividly.
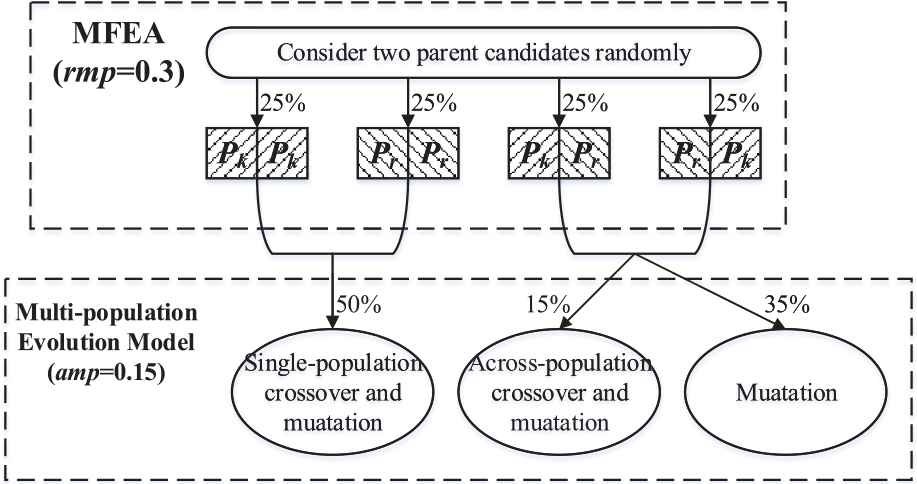
Role of two key parameters in different multi-factorial evolutionary algorithm (MFEA) algorithms.
To make a fair comparison, other parameters used in SBX and polynomial mutation are the same for sp-MFEA and mp-MFEA. Furthermore, 100,000 function evaluations (the total population size is 100, and the number of maximum iteration is 1000) is adopted as the termination condition. In order to eliminate statistical errors, each algorithm conducts 100 independent runs on each MTO problem.
4.3. Experimental Results
It is emphasized again that, the main purpose of this paper is to provide theoretical and experimental evidence to support the idea that sp-MFEA can be explained and executed as multi-population evolution model. Thus, it is not necessary to compare mp-MFEA separately with the state of the art other EAs. That is to say, if sp-MFEA is superior to any other competitor, we have every reason to believe that mp-MFEA is also superior to that one.
The experimental results on 25 MTO problems are provided in Table 3.
| MTO Problem | Task | sp-MFEA | mp-MFEA | Error(%) |
|---|---|---|---|---|
| 1 | T1 | 0.3722 | 0.3712 | −0.2687 |
| ±0.06208 | ±0.06245 | |||
| T2 | 196.2531 | 197.8287 | 0.8028 | |
| ±39.2357 | ±43.9761 | |||
| 2 | T1 | 4.5929 | 4.7939 | 4.3763 |
| ±0.6896 | ±0.9310 | |||
| T2 | 230.3932 | 233.1326 | 1.189 | |
| ±52.8207 | ±53.3635 | |||
| 3 | T1 | 20.186 | 20.1783 | −0.0381 |
| ±0.08046 | ±0.08111 | |||
| T2 | 3702.7842 | 3705.324 | 0.0686 | |
| ±435.8346 | ±442.5599 | |||
| 4 | T1 | 602.8853 | 591.9885 | −1.8074 |
| ±120.7635 | ±110.4832 | |||
| T2 | 9.4473 | 8.7615 | −7.2592 | |
| ±2.1345 | ±1.7955 | |||
| 5 | T1 | 3.5523 | 3.6058 | 1.5061 |
| ±0.5926 | ±0.5562 | |||
| T2 | 697.7636 | 693.0246 | −0.6792 | |
| ±261.5233 | ±255.1908 | |||
| 6 | T1 | 19.9451 | 19.8801 | −0.3259 |
| ±0.7805 | ±1.4307 | |||
| T2 | 20.2608 | 21.1484 | 4.3809 | |
| ±2.4460 | ±3.1628 | |||
| 7 | T1 | 951.3895 | 894.6049 | −5.9686 |
| ±484.5731 | ±623.0197 | |||
| T2 | 283.7447 | 279.7397 | −1.4115 | |
| ±92.7225 | ±93.0268 | |||
| 8 | T1 | 0.4139 | 0.4095 | −1.0631 |
| ±0.06906 | ±0.07272 | |||
| T2 | 26.9026 | 26.6582 | −0.9085 | |
| ±2.8228 | ±2.9572 | |||
| 9 | T1 | 627.5886 | 604.3195 | −3.7077 |
| ±114.6623 | ±130.6374 | |||
| T2 | 3683.4686 | 3750.888 | 1.8303 | |
| ±404.4735 | ±483.9195 | |||
| 10 | T1 | 691.4073 | 701.2433 | 1.4226 |
| ±0.06149 | ±0.06294 | |||
| T2 | 887.2425 | 883.8248 | −0.3852 | |
| ±0.5208 | ±5.1133 | |||
| 11 | T1 | 693.9376 | 701.2482 | 1.0535 |
| ±0.1102 | ±0.09062 | |||
| T2 | 1228.9126 | 1200.258 | −2.3317 | |
| ±0.09984 | ±0.06575 | |||
| 12 | T1 | 690.1628 | 701.2613 | 1.6081 |
| ±0.1845 | ±0.08907 | |||
| T2 | 1552.9553 | 1536.98 | −1.0287 | |
| ±11.2278 | ±10.5782 | |||
| 13 | T1 | 851.4715 | 831.112 | −2.3911 |
| ±4.0491 | ±4.7456 | |||
| T2 | 1566.3998 | 1536.776 | −1.8912 | |
| ±10.0199 | ±9.1995 | |||
| 14 | T1 | 1211.3314 | 1189.84 | −1.7742 |
| ±50.4861 | ±47.584 | |||
| T2 | 1767.7217 | 1856.799 | 5.0391 | |
| ±225.8596 | ±241.5125 | |||
| 15 | T1 | 1202.806 | 1215.996 | 1.0966 |
| ±47.713 | ±52.7256 | |||
| T2 | 6338.8597 | 6721.543 | 6.0371 | |
| ±750.7684 | ±794.1648 | |||
| 16 | T1 | 1760.2002 | 1809.771 | 2.8162 |
| ±255.2642 | ±261.4864 | |||
| T2 | 1556.9887 | 1619.849 | 4.0373 | |
| ±0.6051 | ±0.7181 | |||
| 17 | T1 | 6918.7345 | 7067.598 | 2.1516 |
| ±627.7413 | ±763.0831 | |||
| T2 | 1299.8032 | 1300.566 | 0.05869 | |
| ±0.8912 | ±0.10962 | |||
| 18 | T1 | 1297.0837 | 1300.604 | 0.2714 |
| ±0.1242 | ±0.1086 | |||
| T2 | 1396.0996 | 1400.401 | 0.3081 | |
| ±0.169 | ±0.1895 | |||
| 19 | T1 | 1402.1645 | 1400.395 | −0.1262 |
| ±0.2227 | ±0.20471 | |||
| T2 | 1558.4454 | 1619.672 | 3.9287 | |
| ±0.5257 | ±0.654 | |||
| 20 | T1 | 0.3949 | 0.3914 | −0.8923 |
| ±0.09946 | ±0.05741 | |||
| T2 | 219.3648 | 214.9281 | −2.0225 | |
| ±60.3468 | ±51.6896 | |||
| T3 | 2.9733 | 3.0568 | 2.8094 | |
| ±0.2498 | ±0.4617 | |||
| 21 | T1 | 4.5455 | 4.7334 | 4.1328 |
| ±1.008 | ±0.8037 | |||
| T2 | 250.3884 | 253.1382 | 1.0982 | |
| ±48.891 | ±55.4667 | |||
| T3 | 11.2499 | 11.6872 | 3.8876 | |
| ±1.825 | ±1.7124 | |||
| 22 | T1 | 296.2614 | 288.745 | −2.5371 |
| ±100.1678 | ±89.8639 | |||
| T2 | 12.4034 | 11.7768 | −5.0517 | |
| ±3.0553 | ±2.7105 | |||
| T3 | 1154.5031 | 1103.511 | −4.4168 | |
| ±589.3421 | ±516.4512 | |||
| 23 | T1 | 3.7924 | 3.9066 | 3.012 |
| ±0.5793 | ±0.6347 | |||
| T2 | 1129.359 | 1075.021 | −4.8114 | |
| ±980.7422 | ±899.4705 | |||
| T3 | 9.8274 | 9.8191 | −0.08427 | |
| ±1.7825 | ±1.6221 | |||
| 24 | T1 | 1291.5757 | 1258.213 | −2.5831 |
| ±850.1225 | ±782.4116 | |||
| T2 | 309.8185 | 303.9567 | −1.892 | |
| ±99.7586 | ±102.2846 | |||
| T3 | 0.506 | 0.49818 | −1.536 | |
| ±0.05174 | ±0.07614 | |||
| 25 | T1 | 0.4806 | 0.4751 | −1.139 |
| ±0.08905 | ±0.07231 | |||
| T2 | 26.4804 | 28.079 | 6.037 | |
| ±3.4817 | ±3.0328 | |||
| T3 | 13.3453 | 12.6569 | −5.1581 | |
| ±5.7749 | ±2.8255 |
MFEA = multi-factorial evolutionary algorithm; MTO = multi-task optimization.
Mean performance of two MFEA algorithms on 25 MTO problems.
From Table 3, the average best results obtained by two algorithms, sp-MFEA and mp-MFEA, are similar to each other. Not surprisingly, the same conclusion applies to all test suites: standard MTO problems, complex MTO problems, and 3-task MTO problems. In most cases, the relative error is less than 5% as shown in the last column of Table 3. The performance difference between the two algorithms over all MTO benchmark problems is not statistically significant at p < 0.05 (Wilcoxon rank-sum). These results demonstrate that multi-population evolution model is very credible within an easy-to-understand configuration.
4.4. More Discussion
Compared with sp-MFEA, the other advantage of mp-MFEA is that it provides an opportunity to analyze the evolution process of subpopulations. For instance, for each individual
In order to answer this question exactly, take MTO problem 1 as an example, the number of individuals and improved individuals (its function fitness is smaller than its parent's) and the ratio of improved individuals in three groups are recorded as shown in Figures 5–7, respectively. As is clear from Figure 5, each event's probability fluctuates slightly over generations (population size is 100 in this paper). The average probability for each group is 50%, 15%, and 35%, respectively, which coincide with the theoretical probability as shown in Figure 4.
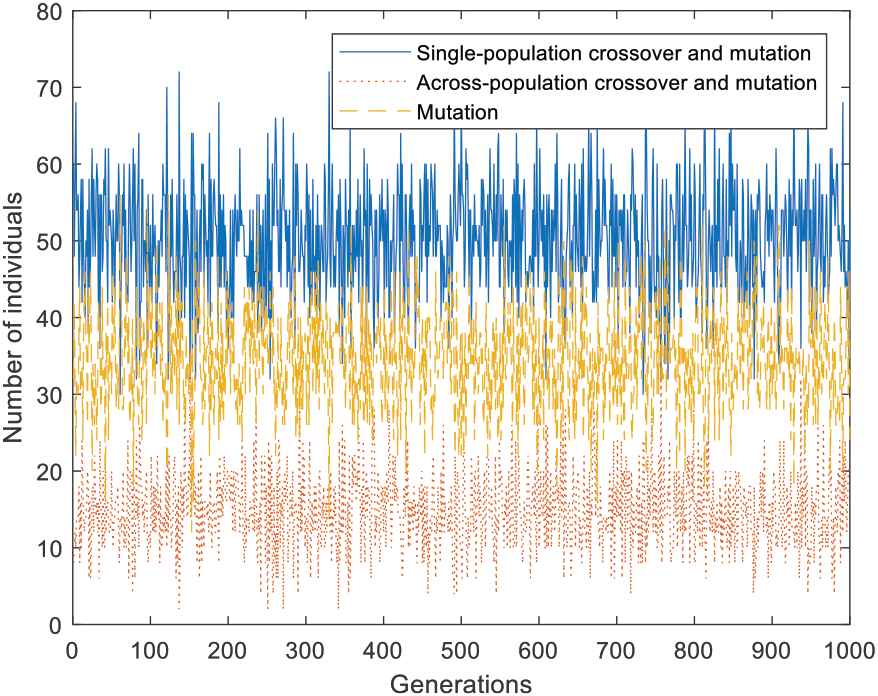
Number of individuals in different groups for multi-task optimization (MTO) problem 1.
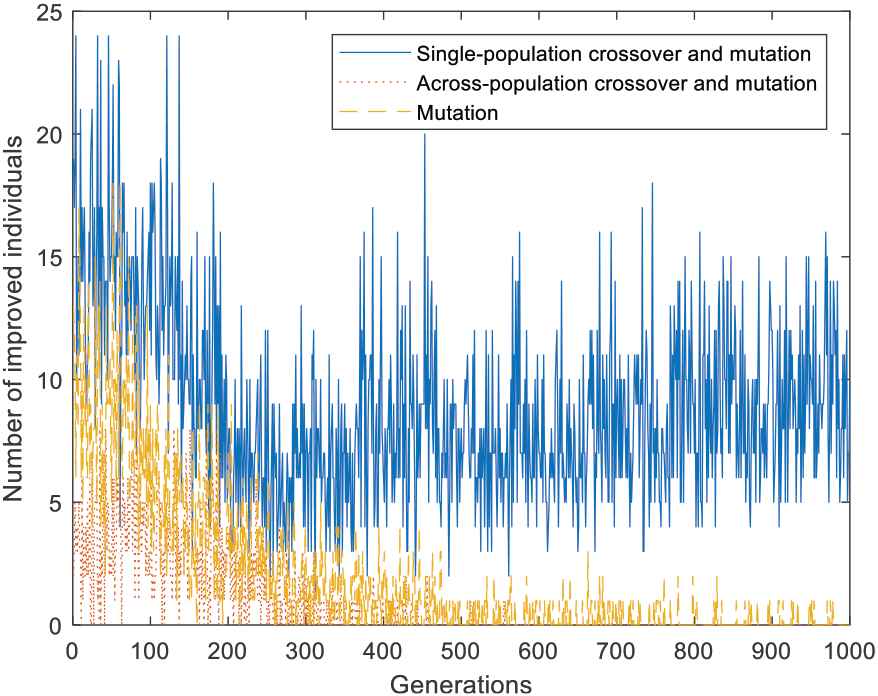
Number of improved individuals in different groups for multi-task optimization (MTO) problem 1.
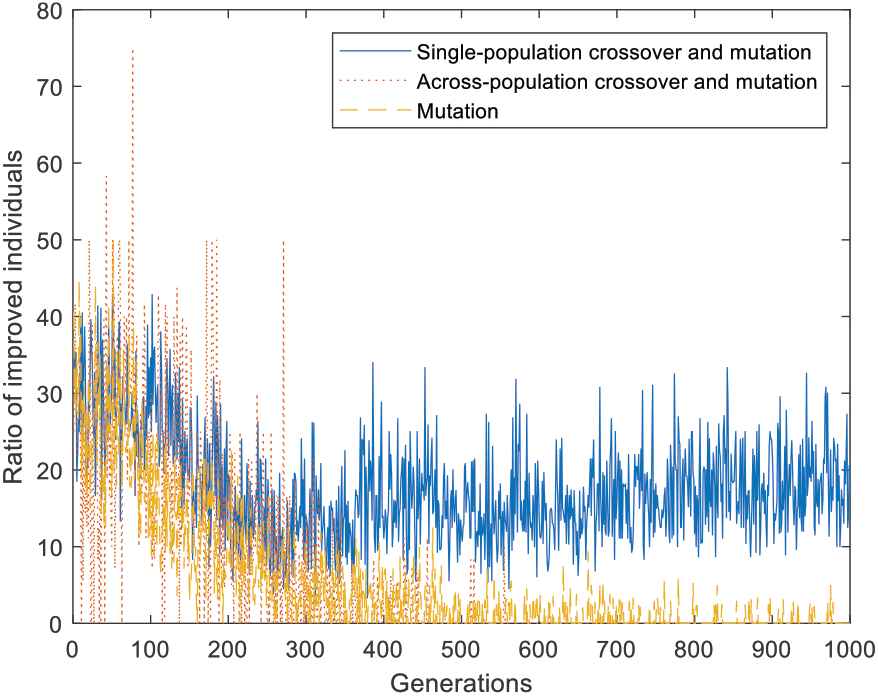
Ratio of improved individuals in different groups for multi-task optimization (MTO) problem 1.
Figure 6 reveals the number of improved individuals also changes continually over generations. It declines slowly during the initial 400 generations and then moves towards stabilization. Comparatively speaking, both the number and the ratio of improved individuals in group 1 is the largest among three groups from Figures 6 and 7. In this run, the average number and the average ratio is 8.91 and 17.75%, respectively. As a result, we can conclude that individuals underwent single-population crossover and mutation have the greatest contribution to improve the algorithm performance.
Notice from Figure 7, at the beginning of population evolution, the ratio of improved individuals underwent across-population crossover and mutation is high (although unstable). However, the number of improved individuals in group 2 is almost zero at the end of this run, as shown by Figure 5, which means it has zero (even negative) effect to advance the algorithm performance. Thus a research direction in future is to adjust the occurrence probability of different reproduction operators adaptively.
Unfortunately, for classic sp-MFEA, each individual may come from any tasks and change over and over during population evolution. Therefore it is impossible to analyze the corresponding contribution of each group as shown above.
5. CONCLUSION
While some people agree that MFEA is seen as a novel multi-population EA for MTO, wherein each subpopulation is represented independently and evolved for its own task only, it is an intuitive or even mediumistic idea. In this study, we make an in-depth analysis of the coincidence relation between multi-population evolution model and MFEA.
Firstly, in order to clear up potential misunderstandings, we answer several key questions unsettled to date, and design a novel across-population crossover approach to avoid population drift. Then MFEA and its variation are reviewed carefully in view of multi-population evolution model, and the coincidence relation between them are concluded. These analysis results provide more evidence to support the opinion by Hashimoto in [8].
Massive experimental results on sp-MFEA and mp-MFEA also reveal our work's rationality and superiority. What is even more important is that, with the help of it, we can analyze the evolution process precisely and then design more efficient multi-population EA for MTO. From experimental results, we notice that individuals from a different group may have positive, zero, or negative contribution to improve the algorithm performance.
We will seek the hidden reason and find an effective way to adjust the intensity of knowledge transfer adaptively. In the future, following multi-population evolution model, we also hope to predict theoretically the effect of the parameters and genetic operators of MFEA on the quality of global solutions.
CONFLICT OF INTEREST
The authors have declared no conflict of interest.
AUTHORS' CONTRIBUTIONS
Na Wang: literature search, study design, data collection; Qingzheng Xu (corresponding author): study design, manuscript writing, data analysis, critical revision of the article; Rong Fei: study design, manuscript writing, data collection; Jungang Yang: literature search, study design; Lei Wang: data analysis
ACKNOWLEDGMENTS
This work was supported in part by the National Natural Science Foundation of China (Grant no. 61773314); the Shaanxi Science and Technology Project (Grant no. 2017CG-022); and the Scientific Research Foundation of the National University of Defense Technology (Grant no. ZK18-03-43).
REFERENCES
Cite this article
TY - JOUR AU - Na Wang AU - Qingzheng Xu AU - Rong Fei AU - Jungang Yang AU - Lei Wang PY - 2019 DA - 2019/10/14 TI - Rigorous Analysis of Multi-Factorial Evolutionary Algorithm as Multi-Population Evolution Model JO - International Journal of Computational Intelligence Systems SP - 1121 EP - 1133 VL - 12 IS - 2 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.191004.001 DO - 10.2991/ijcis.d.191004.001 ID - Wang2019 ER -
