Optimized Differential Evolution Algorithm for Software Testing
- DOI
- 10.2991/ijcis.2018.125905642How to use a DOI?
- Keywords
- Software testing; Test data generation; Differential evolution algorithm; Premature convergence; Anti-aging; Rebirth strategy
- Abstract
Differential evolution (DE) algorithms for software testing usually exhibited limited performance and stability owing to possible premature-convergence-related aging during evolution processes. This paper proposes a new framework comprising an antiaging mechanism, that is, a rebirth strategy with partial memory against aging, for the existing DE algorithm and a specialized fitness function. The results of application of the proposed framework to instantiate three DE algorithms with different mutation schemas indicate that it significantly improved their effectiveness, performance, and stability.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
As a well-known heuristic algorithm, the differential evolution (DE) algorithm is becoming increasingly popular and important owing to its quick convergence, robustness, and simplicity [1]. It has thus been employed in the domains of constrained optimization [2, 3], multiobjective optimization [4, 5], and filter design [6], among others.
The use of the DE algorithm is also spreading into the domain of search-based automatic software testing. For example, a test data generator (TDG) was proposed by taking the DE algorithm as the core to solve the constrained optimization problem [7], and different algorithms were compared and evaluated, demonstrating the immense potential of DE in solving constrained optimization problems. For branch testing, both the genetic algorithm (GA) and DE were demonstrated to be effective for test data generation if coupled with the path prefix strategy, memory, and elitism [8]. Based on the function minimization strategy [9, 10], the DE algorithm was improved for automatic generation of test data using “branch function superposition” as a fitness function. DE can be merged with the ant colony algorithm for combinatorial testing to determine the minimum test case set [11]. The quantum-inspired multi-objective differential evolution algorithm (QMDEA) was proposed by combining DE with quantum computation to minimize a multi-objective test set [12].
However, some challenges remain to be addressed: 1. The DE algorithm itself may also demonstrate a prematurity phenomenon by being trapped in the local optimum, similar to many other heuristic algorithms. 2. For coverage-oriented software testing, the complex code logic may also allow many different test data to fall into the same equivalence class, which results in meaningless test cases that have no contribution to the coverage increase. These two factors can together strongly further amplify the possibility of premature convergence for DE in the context of software test data generation to achieve the objective of greater coverage with fewer test cases, especially for programs with complex structures.
The main contribution of this paper is the presentation of the design of a new framework for optimized DE algorithms to achieve more stable results with high performance and effectiveness for coverage-oriented software testing. The framework is realized by a new rebirth strategy with partial memory for the existing DE algorithm, and a specialized fitness function to account for the increase in accumulated coverage during the entire testing process. This proposed method is then applied to instantiate three DE algorithms with different mutation schemas and then to form three new optimized DE algorithms: rebirth of differential evolution algorithm (DE-R), rebirth of optimal vector differential evolution algorithm (OVD-R), and rebirth of double differential evolution algorithm (DDE-R). Through experimental studies on seven programs from the Siemens program set, we noted that all the optimized DE algorithms provided significant improvement; better effectiveness, performance, and stability was demonstrated when the proposed method was adopted, even though different mutation factors were observed.
2. RELATED WORK
Many methods have proved to be effective in coverage-oriented test data generation by meta-heuristic searching [7, 13–15]. For example, an improved DE algorithm for automated test case generation for path coverage (ATCG-PC) was proposed in Ref. [16] along with the use of a self-adaptive fitness function and a modified DE algorithm to apply more heuristic information to generate a greater number of uncovered paths with fewer test cases. An approach based on the one-test-at-a-time strategy DE algorithm was proposed in Refs. [17, 18] to generate a test suite with a smaller scale. The authors observed and studied the effects of various parameters on the optimization algorithm performance, proving that the scale of the combinatorial test suite generated by the DE algorithm is smaller than those of other commonly used methods. Based on the analyses presented in Refs. [7, 13], it was found that DE outperformed the GA, binary genetic algorithm (BGA), and artificial bee colony (ABC) for generating test data in less time and had better coverage in fewer generations. Specifically, it was shown that the parameter setting of the scaling factor F and CR rate plays a major role for DE. The optimized solution for DE-based software testing proposed herein was verified to be always effective for different parameters and strategy settings. Some approaches were verified as being effective when coupled with the strategy of a path prefix, memory, and elitism [8]. The memory strategy herein means that, each time a branch is traversed for the first time, the corresponding test data that traverse this branch should be stored and injected into the population when the sibling branch is selected for traversal. Unlike our partial-memory rebirth strategy without many extra storage constraints, it is a totally memory-based solution, which requires the storing of all the mappings of branches and their corresponding data.
For the restart mechanism, the most closely related work involves RDEL, a new version of the DE algorithm, which was presented based on a couple of local search mutations and a restart mechanism for numerical optimization problems over a continuous space [19]. For RDEL, to avoid stagnation or premature convergence, the proposed restart mechanism is combined with a random mutation scheme and a modified breeder genetic algorithm (BGA) mutation scheme by increasing the crossover probability and uniform scaling factors, although both approaches share the same philosophy to focus on the rebirth mechanism. The main differences are as follows: 1. The rebirth mechanism is different. The restart mechanism of RDEL is based on the combination of random mutations and a modified BGA. It can be viewed as a local restart mechanism for different mutation strategies. Our proposed rebirth strategy is in fact a light-weight and global rebirth mechanism without complex parameter tunings, which is more feasible for practical applications. 2. The effectiveness of RDEL only can be manifested by integrating many different parts including (a) a novel local mutation rule inspired by PSO, which should also be combined with the basic mutation strategy through a linear decreasing probability rule; (b) the exponent increased crossover probability, which should be utilized to balance the global and local exploitation; and (c) the random mutation scheme and a modified BGA mutation scheme, which should be merged to avoid stagnation and/or premature convergence. 3. The application domain is different; that is, RDEL is used for numerical optimization problems, and the proposed scheme is used for coverage-oriented software testing. The above factors imply that, if RDEL is to be applied for specific different application domains, there is still considerable work required to overcome its complex parameter configuration or strategy combination, which should be more self-adaptive.
3. PROPOSED METHOD TO OPTIMIZE DE FOR SOFTWARE TESTING
In this section, we introduce the general process of DE-based software testing, the aging problem of the traditional DE-based approach, the proposed method for solving this problem (rebirth strategy), and the fitness function design criterion.
3.1. DE-Based Approach for Software Testing
DE algorithms have been used in several domains since being introduced by Ken Price and Rainer Storn [20], including software testing [21]. The process of automatically generating software test data based on DE is as follows: Before the beginning of the evolution, the termination evolution condition (including the termination fitness function and the maximum evolution iterations), the fitness function, and the algorithm parameters are given. At the beginning of evolution, the population is first initialized by a method such as random generation to generate the initial population. Subsequently, the fitness function and evolutionary iteration of the initial population are calculated for determining whether evolution must be stopped. If the termination condition is not reached, the differential mutation, crossover, and selection operations are performed to generate a new population, and the evolution termination judgment is re-executed until all termination conditions are met. In DE-based software testing, an individual is a set of test input data, the population is the test data set, and the coverage of the test data set (such as branch coverage) is used as the fitness function. Figure 1 shows the flowchart of the traditional DE algorithm used for software testing.
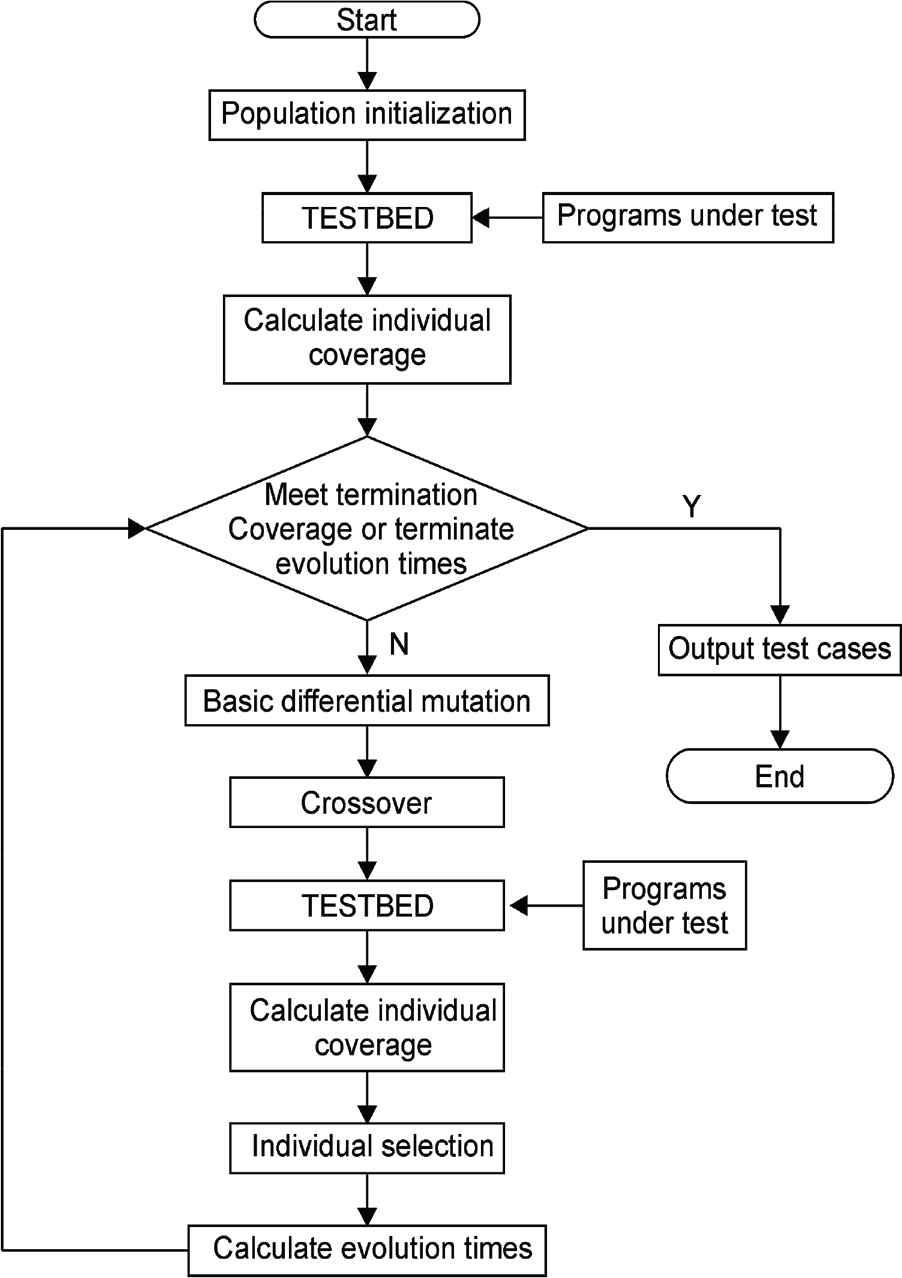
Flowchart of traditional differential evolution (DE) for test data generation: “TESTBED” is a software for coverage computing.
3.2. Problem Description: Aging of DE-Based Software Testing
DE algorithms have been used for testing data generation because of their excellent search effectiveness for nonlinear optimization. First, the initial individuals are generated randomly. As the population evolves, the initial individuals will experience the crossover operation, mutation operation, and selection operation with certain probabilities. The population gradually moves toward the optimal solution. This process usually ensures that the elite solution will not disappear during the evolution process; however, since the individuals in the population will become increasingly similar, their crossover and selection may not play a role in the following evolution process, which means that the local population is subjected to prematurity, and the coverage stops increasing in the context of complex software testing.
Definition 1. (PopulationAging):
When the population evolves t generations, the cumulative coverage no longer increases even if another Δt generations are being evolved. That is, we cannot find new effective test cases through the evolution of the current population after t generations have evolved. Referring to the definition of software aging [22], this situation is termed population aging of DE-based software testing.
Definition 2. (PopulationDiversity):
We use PopulationDiversity to represent the similarity of the items in the current population. Further, we define PopulationDiversity = Ndif/ Npop, where Ndif is the number of different items in the population, Npop is the population size, and 0 ≤ Ndif ≤ Npop. Therefore, PopulationDiversity = 0 if all the items are the same and; PopulationDiversity = 1 if all the items are totally different; otherwise, PopulationDiversity ∈ (0, 1) aligns to their degree of similarity.
Definition 3. (LocalOptimism):
If the best solution is not found, and DE is stagnated in a local solution in continuing k generations, the current solution is termed LocalOptimism.
Definition 4. (GlobalOptimism):
If the best solution is noted to satisfy the required fitness or other criteria, this final solution is termed GlobalOptimism.
When PopulationDiversity = 0 or is small enough in continuing k generations, irrespective of the number of mutations and crossovers operated, further fitness increment either cannot be achieved or is difficult to be achieved, based on the current populations, which means that the algorithm of DE is trapped in the state of the local or global optimism solution. If the probability of PopulationDiversity is increasing, then that of LocalOptimism may decrease and that of GlobalOptimism may increase. Through analysis, we determined that there are two main reasons for the resulting aging phenomenon for DE-based software testing: 1. Reduction of PopulationDiversity. For the evolutionary algorithm, including the DE algorithm, the evolution of the population involves generating new individuals based on the original individual; therefore, there is a trend of convergence between individuals. That is to say, in the later stages of evolution, the differences between individuals will gradually decrease, which leads to the decrease in PopulationDiversity, and the DE algorithm is easily falls into LocalOptimism. 2. Unevenness of the solution space distribution. In the process of evolution of test cases, the newly generated test cases will fall in the vicinity of the points that have been inevitably searched in the solution space, which leads to unevenness of that distribution. If the test cases corresponding to the branches that have not yet been covered are distributed in the space that is far apart from the space of the individual convergence, especially in the boundary space of the solution space, new effective test cases may not be found even through repeated evolutions [23].
Therefore, the population aging of DE for software testing can be divided into three categories: local aging, global aging, and domain aging, and these can be described as follows: 1. Local aging: The PopulationDiversity of a new population may become sufficiently small after t generations of evolution, and irrespective of the number of mutations and crossovers operated, the cumulative coverage no longer increases. In other words, we cannot find new effective test cases through the evolution of current populations, while the GlobalOptimism is still not satisfied. Hence, we name the DE algorithm in such a LocalOptimism state as local aging. 2. Global aging: The GlobalOptimism is not satisfied, even though all possible LocalOptimism are obtained through different DE evolution processes. In other words, the evolved population cannot further increase the number of objects through some antiaging actions, although the GlobalOptimism state is still not achieved. This situation is called global aging. 3. Domain aging: The aging state of a population between local aging and global aging is domain aging, which arises from the application domain. It is not in a state of local or global optimism, and instead, is in an equivalent state or region for continue k generations for a long time, the situation is termed domain aging. Local Optimism can cause domain aging, but domain aging does not imply Local Optimism.
From the above analysis, we can see that during the traditional DE evolution process, most of the population tends to have similar gene fragments, which makes the crossover operation and the selection operation lose the function of further optimization. The populations gradually tend toward aging. We hope that, after reaching certain steps, the coverage can continue improving against this aging obstacle through some special but simple mechanism.
3.3. Proposed Strategy: Rebirth With Partial Memory Against Aging
In this section, we describe the design of an antiaging mechanism by adopting a rebirth strategy with partial memory for DE-based software testing (Figure 2). When the population evolution process steps into the local aging status, a rebirth action will be triggered and then the population will be completely destroyed. The new population, which can increase the coverage, will be generated to conquer the local aging or domain aging. This rebirth evolution process will be iterated until the global aging or global optimism state is obtained (Figure 3). Rebirth with partial memory means that any new generated individual can only be selected as the initial population for the new rebirth evolution if and only if it can contribute to the subject-object. Rebirth without memory means that a simple restart mechanism will be triggered when the local aging condition is detected. Here, we select the strategy of rebirth with partial memory as the antiaging mechanism because we believe that any elite individual has manifested its values in the local DE evolution process, and it is meaningless to try the process again in the new rebirth evolution process.
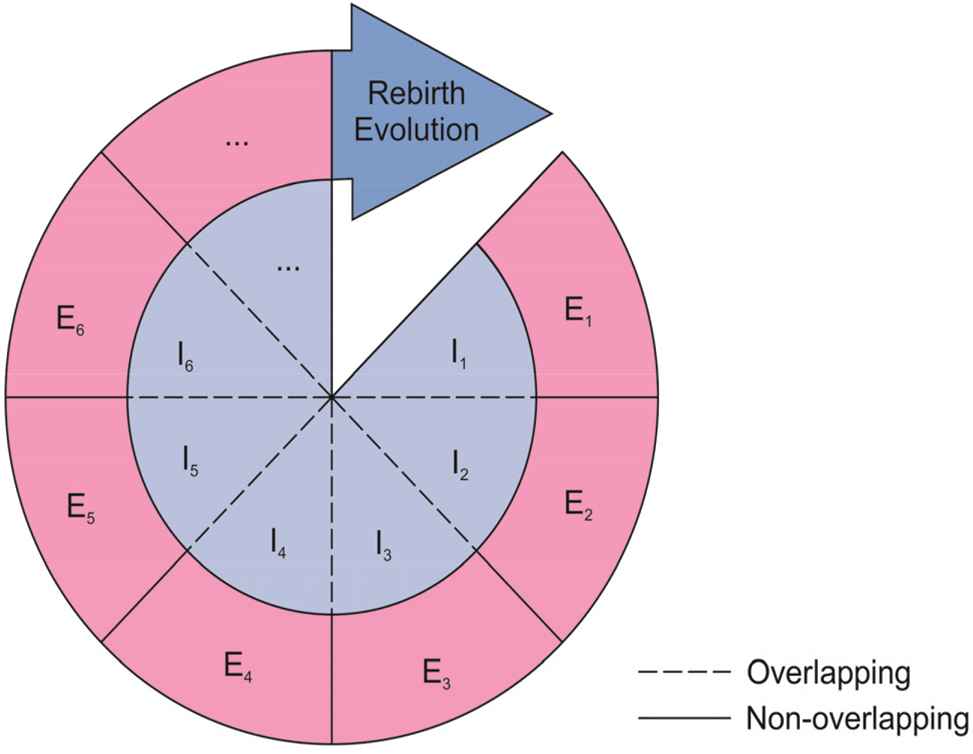
Mechanism of rebirth evolution with partial memory: “E” represents the effective test data that can increase the cumulative coverage and “I” represents invalid test data that have no contribution to the cumulative coverage increase. The numbers represent the generations of evolution iterations. The results of the partial-memory strategy indicate that the effective test cases generated by each rebirth will not overlap, and only the invalid test cases may overlap.
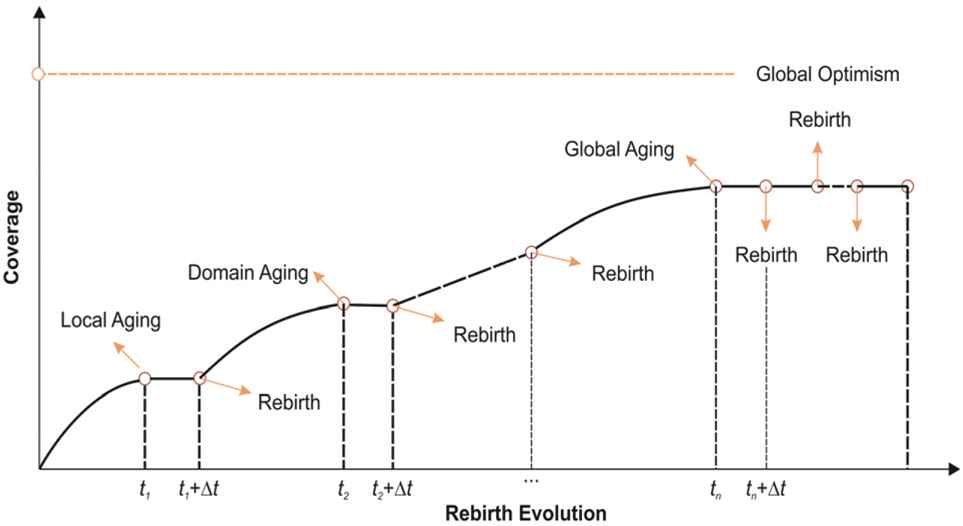
Process of antiaging by rebirth evolution: “t” represents the time of evolution iteration, and “Rebirth” represents q ≥ qmax in that time and the rebirth condition is triggered.
In order to determine the triggering conditions for population rebirth, the aging factor q is used to indicate the extent of population aging. We define the aging factor as the percentage rate of the number of new test cases without contributing to coverage promotion in generations from the total number of previous test cases.
We set Npopt to the individuals’ number of tth populations, and ni,j is the dimension of the ith individual in the jth population; therefore, the total number of test cases that are generated through t generations of evolution is
With the increase in Δt, aging factor q increases. Here, q can be greater than 1, and a larger q represents a highest degree of population aging. At the same time, given a threshold qmax for aging factors, the rebirth condition is triggered once q ≥ qmax, and the entire population is destroyed. Then, the new population is regenerated and continues to evolve until the conditions of evolutionary termination are met.
For DE-based software testing, the test cases that can increase the cumulative coverage are the effective test cases, which comprise the set of E. The set of invalid test cases is designated as I, and these have no contribution to the cumulative coverage increase. Therefore, aging factor q can also be defined as the ratio of invalid test cases to effective test cases, that is,
The rebirth condition is triggered once q ≥ qmax; then, the new population is regenerated, the population continues to evolve, and the effective test case set E2 and invalid test case set I2 are generated. We adopt the strategy of rebirth with partial memory against the population aging proposed in this paper (Figure 3). The algorithm remembers all the test cases in the effective test case set E before rebirth, and the test cases generated after rebirth will be matched with the existing effective test cases. If the new test case is the same as the existing one or belongs to the same equivalent class, the new test case belongs to I2, rather than E2. The results of the partial-memory strategy are that the effective test cases generated by each rebirth will not overlap, and only the invalid test cases may overlap (Figure 2). We can obtain E = E1 + E2, I = I1 + I2 − I1 I2. The second and later rebirth is similar to the first rebirth.
When the population evolution process steps into the local aging status, the accumulated coverage cannot be increased further; however, the ideal acquired coverage has not been obtained. When q is set to the aging factor, it indicates the percentage rates of the number of new test cases without contributing to the coverage promotion in Δt generations from the number of the previous total of test cases. The rebirth condition will be triggered when the aging factor is greater than a certain value, after which the population will be destroyed completely. After that, a new population will be generated to replace the old one, which can increase the coverage of the population.
The rebirth strategy set is defined as follows:
We set qm to the mutation factor, qc to the crossover factor, and M to the overlap of the rebirth population and the old population. According to the assumption of the aging factor, some of the test cases do not influence the coverage. Therefore, when we do not use the rebirth strategy, the increment of the test cases from the Δtth generation to the Δt + 1th generation is approximately
For comparison, we obtain the difference value by subtracting the incremental test cases of the DE algorithm from those of the rebirth algorithm. When the data styles of the chromosomes are Boolean and binary, the expectation of M reaches its maximum value. Here, M equals
Because
3.4. Fitness Function Design: Increment of Accumulative Coverage
Coverage-oriented software testing usually involves statement coverage, branch coverage, condition coverage, and path coverage, among others. Among these, branch coverage requires a large number of test cases to ensure that each judgment of the program could be true at least once and false at least once. As a result, the branch coverage has more testing paths and has stronger testing abilities. We choose branch coverage as the object in our test, as is shown in Equation (5). In the equation, Covc is branch coverage, T is the increment number of executed branches, and Tall is the total number of branches.
In Equation (6), fi is the individual fitness calculated by branch coverage.
4. THREE INSTANTIATED ALGORITHMS: RESULTING OPTIMIZED DE ALGORITHMS FOR SOFTWARE TESTING
In this section, we introduce the three improved algorithms and present their processes of implementation in detail. When the rebirth strategy is applied to the traditional DE algorithm, the rebirth differential evolutionary algorithm appears. The rebirth strategy will be triggered when the population is caught in the local optimal solution, and it will generate a new population as parent individuals to avoid prematurity. The differential mutation factors of the rebirth OVD-R and the rebirth double DE algorithm are DE/best/1/bin and DE/rand/2/bin, respectively, which are introduced in detail in the following section:
4.1. Rebirth of DE Algorithm
Equation (7) is the mutation factor used by the DE-R, and it is the same formula as that used by the classical DE algorithm. The difference between the two algorithms is only in the rebirth strategy. The flowchart of DE-R is shown in Figure 4.
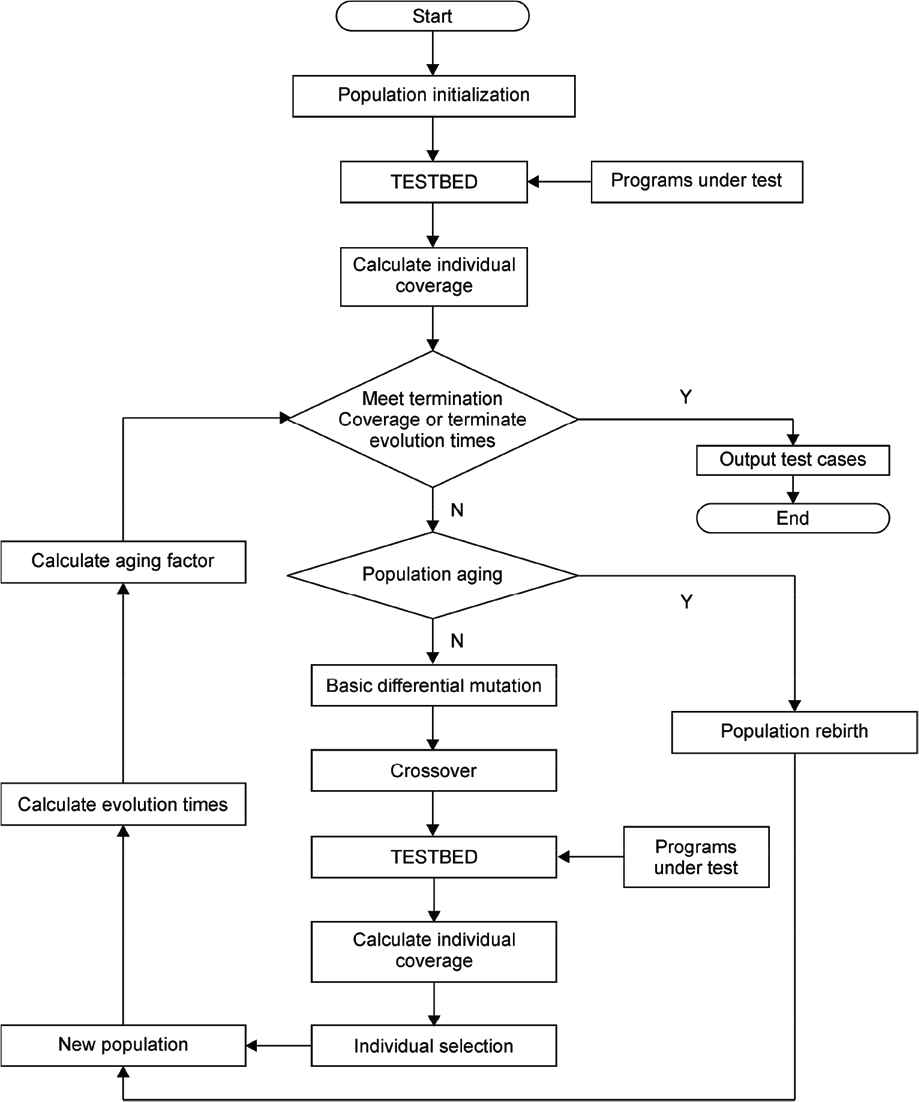
Flowchart of differential evolution algorithm (DE-R) for test data generation:“TESTBED” is a software for coverage computing.
4.2. Rebirth of OVD-R
The OVD-R integrates the optimized rebirth strategy within itself and uses the differential mutation factor DE/best/1/bin in Equation (8) at the same time.
In the equation, Xbes is the optimal individual in the current population, Xi is the parent individual, r2 ≠ r3 ≠ i are two random individuals in the population, Vi is the mutation vector, and F ∈ [0, 2] is the zoom factor.
In Equation (8), the difference between DE/best/1/bin and DE/rand/1/bin is based on whether Xr1 is a random vector or the most optimal individual in the current population. DE/best/1/bin uses the most optimal individual,Xbest, to replace the random vector Xr1, so we can keep the best individual in the mutation vectors at all times. Additionally, this process helps reach convergence more rapidly with less evolution time and finds the best test case more efficiently. However, because the best individual Xbest may not be replaced by other better individuals, Xbest can be regarded as a constant. As a result, the mutation vector only covers two random individuals, which leads to earlier prematurity. Under this condition therefore, the optimized rebirth strategy is more important when we use DE/best/1/bin to replace DE/rand/1/bin for test case generation. The corresponding flowchart is shown in Figure 5.
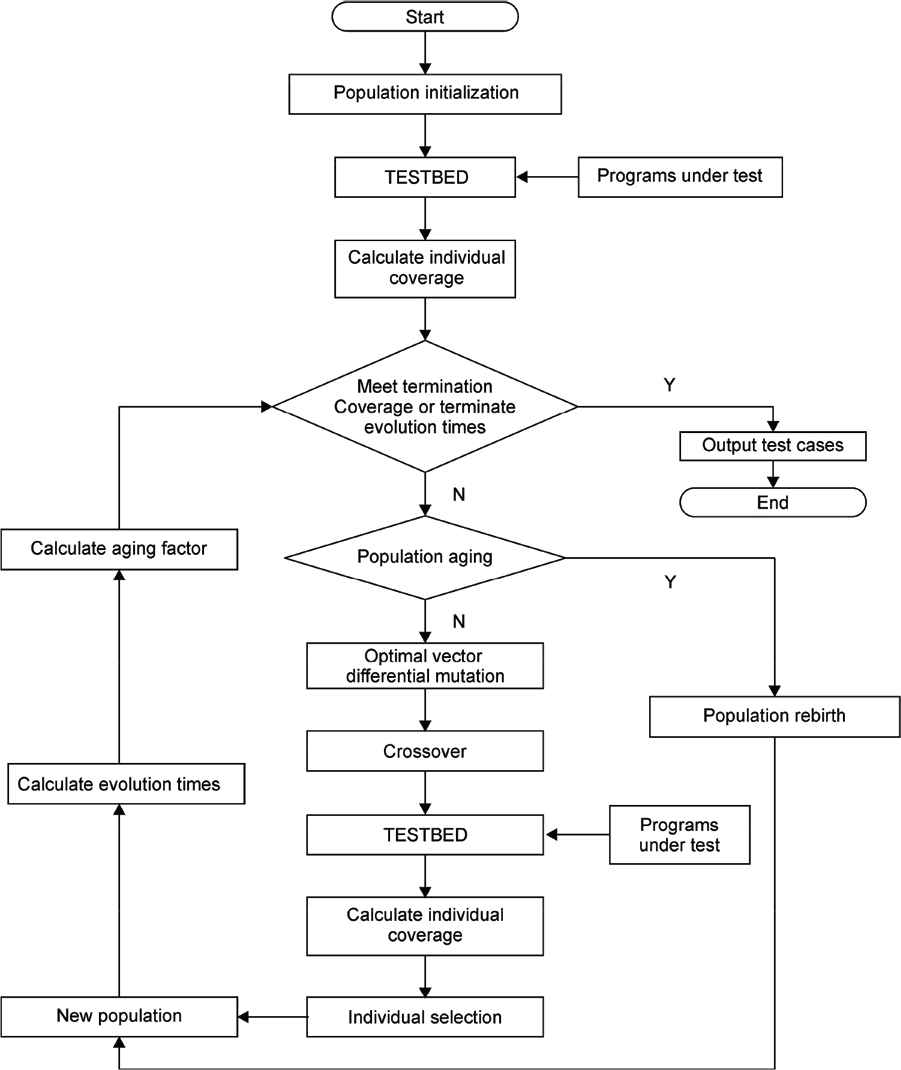
Flowchart of optimal vector differential evolution algorithm (OVD-R) for test data generation: “TESTBED” is a software for coverage computing, and “Optimal vector differential mutation” represents the differential mutation factor: DE/best/1/bin.
4.3. Rebirth of Double DE Algorithm
The DDE-R is similar to OVD-R. It adopts the rebirth strategy and uses DE/rand/2/bin instead of DE/rand/1/bin at the same time to avoid falling into the local premature status. The DE/rand/2/bin mutation factor is shown in Equation (9).
In Equation (9), the difference between DE/rand/2/bin and DE/rand/1/bin is the zoom vector multiplied by F. In DE/rand/1/bin, the vector multiplied by F is the difference between two random vectors, whereas the zoom vector of DE/rand/2/bin is the difference between the sum of two random vectors and that of two other vectors. This procedure increases the independent variables of mutation vector Vi from 3 to 5, and it can further increase the uncertainty of Vi. Compared to DE/rand/1/bin, DE/rand/2/bin can help prevent prematurity during the aging process to some extent. On the contrary, the population may find it more difficult to reach convergence, which means that more evolution generations are required to optimize the population to a specified degree. Moreover, because the two added vectors complicate the algorithm of the mutation vector Vi, the DDE-R algorithm requires more time to generate the same number of test cases. Additionally, preventing the population from experiencing prematurity by increasing the independent variables is closely linked to the population size. If the population is not large enough, this approach may perform unsatisfactorily. Therefore, the rebirth strategy is the main contributing factor in ensuring the superiority of DDE-R over DE in preventing the population from experiencing prematurity and becoming trapped in a local aging status. The flowchart of DDE-R is shown in Figure 6.
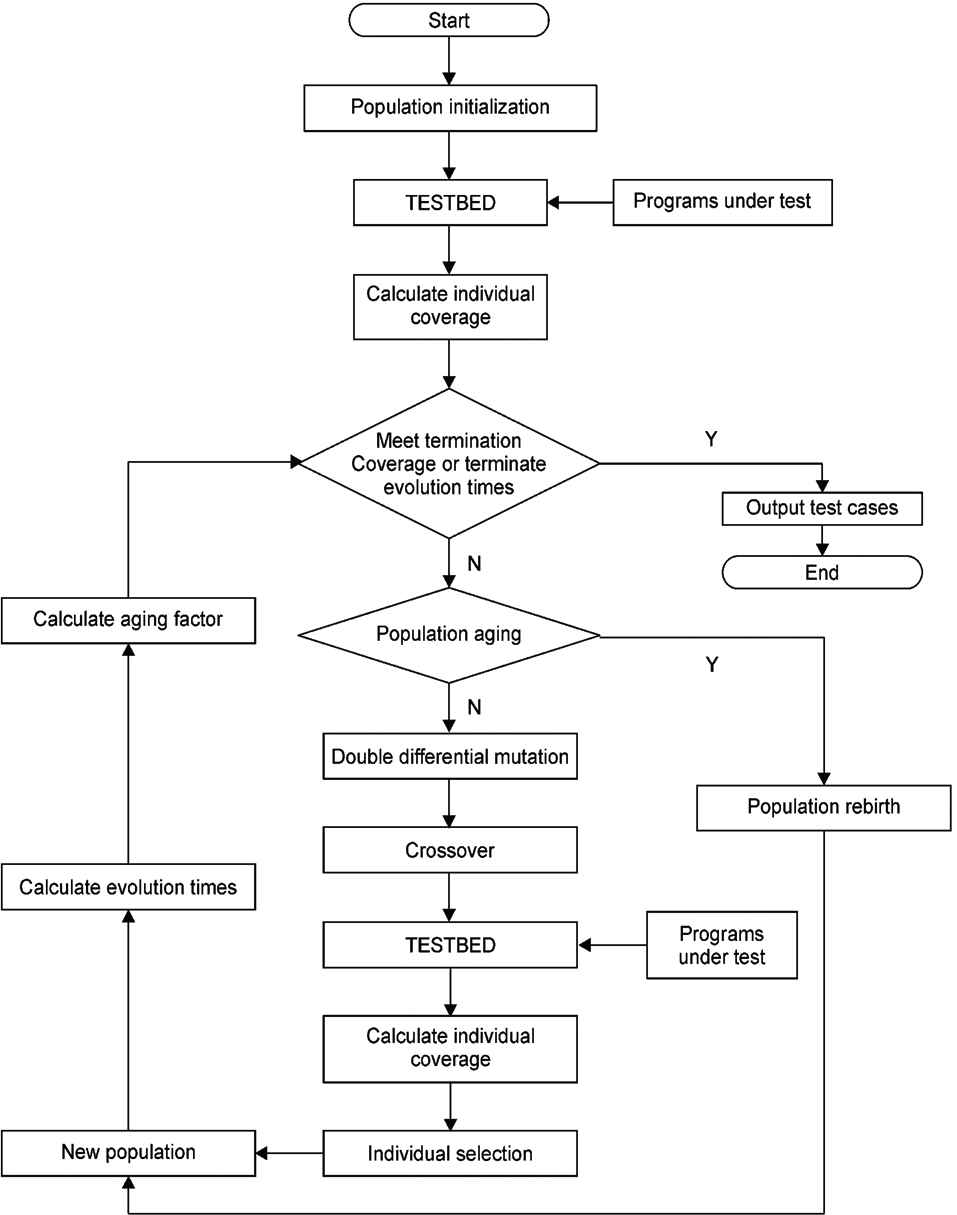
Flowchart of double differential evolution algorithm (DDE-R) algorithm: “Optimal vector differential mutation” represents the differential mutation factor: DE/rand/2.
5. EXPERIMENTAL STUDIES
In this section, we outline our systematic experiments to verify the feasibility and effectiveness of the improved DE algorithms for software testing. Seven programs from the Siemens program set were selected as the subject program under testing, and the automatic testing platform was implemented to support the entire testing process with different algorithms and strategies, including the main components of test data generation, execution, and result collection. Detailed data analysis and results discussion are presented to verify the improved effectiveness and stability from different dimensions.
5.1. Subject Programs Under Testing
According to Refs. [24–26], the Siemens suite is most frequently used as standard experimental test programs, and the size of each program in the suite is small with less than 600 lines of code. Therefore, in this experiment, we selected the classic Siemens program set for the testing programs and downloaded this suite from Ref. [27]. It has seven types of programs: tcas.c, print_tokens.c, print_tokens2.c, tot_info.c, schedule.c, schedule2.c, and replace.c. Even though these programs do not have very large scales, all of them have high complexity (e.g., cyclomatic complexity), which means that they are suitable to be used as the benchmark for coverage-oriented software testing. The basic attributes of the seven programs are listed in Table 1.
| Experimental Object | Lines of Code | Cyclomatic Complexity | Description |
|---|---|---|---|
| tcas.c | 173 | 24 | Preventing aircraft collisions |
| print_tokens.c | 563 | 72 | Printing specific identification |
| print_tokens2.c | 510 | 81 | Printing specific identification |
| tot_info.c | 406 | 24 | Matrix statistics |
| schedule.c | 412 | 33 | Task scheduling |
| schedule2.c | 307 | 40 | Task scheduling |
| replace.c | 563 | 93 | Replacing specific content |
Testing subjects: Siemens program set.
5.2. Experimental Platform
To accelerate the process of experimental studies, we constructed an automatic testing environment for coverage-oriented software testing with different DE algorithms, as shown in Figure 7. This platform mainly includes a test data generation component, a test-driven and coverage-acquired component (TESTBED), and a test data collection component. The test data generation component is the main part that integrates different DE algorithms. Its main function is to model the input interface of the program under testing, and then encode it as the input of the DE algorithm to generate the required test data iteratively. The TESTBED was used to execute the generated test data to drive the program under testing and collect the corresponding program coverage information, which could then be treated as the fitness and feedback to direct further test data generation in the next iteration until the termination condition was satisfied. The test data collection component was used to collect the effective test data during each evolution process for different DE algorithms, which could then be compared for further judgment. This testing platform could be automatically performed, after minimal manual effort and only involved manipulating a few lines of code for each program under testing and different DE algorithms.
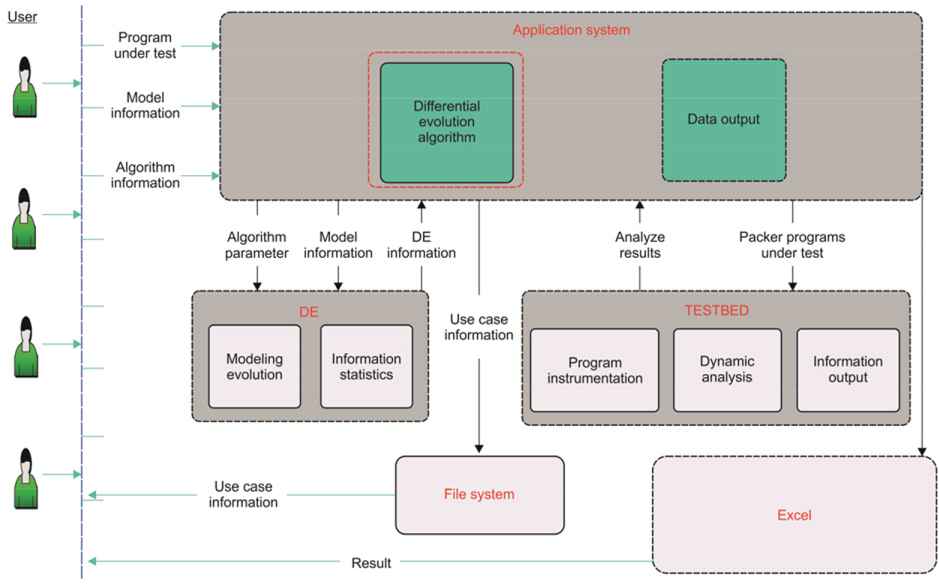
Automatic testing platform: It mainly includes a test data generation component, a test-driven and coverage-acquired component (TESTBED), and a test data collection component.
5.3. Analysis Method
In the experiment, we used four different algorithms, the basic DE algorithm, the rebirth differential evolution algorithm (DE-R), the rebirth OVD-R, and the rebirth DDE-R, respectively, to generate the test cases.
We compared the evolution times and termination coverage of different algorithms to judge the algorithms’ effectiveness and stability. A higher coverage obtained in less time meant higher efficiency. The worst condition was to obtain the least coverage in the longest time. Branch coverage was selected as the measurement of coverage in the experiment. For statistical analysis, each algorithm was tested 10 times for each program to obtain the average value of the observing parameters, and the standard derivation was calculated to judge the stability of the results.
6. RESULTS AND DISCUSSION
In this section, we describe the software testing experiment and analyses of the results of the four algorithms: DE, DE-R, OVD-R, and DDE-R.
The performance of DE algorithms is significantly affected by population size Npop, mutation factor F, and the crossover factor Cr. Moreover, finding bounds for their values has been a topic of intensive research [28]. Ref. [7] proposed a tuning suggestion to assign larger values of population size Npop (around 30) and Ref. [29] presented the rule of thumb values for those parameters: F∈ [0.5, 1.0] and Cr∈ [0.8, 1.0]. Furthermore, Ref. [30] suggested that only high values of Cr can guarantee the contour matching properties of DE, whereas Ref. [31] proved that the mutation scale factor F should not be smaller than
The initial populations of the four algorithms are randomly generated, and the coverage type is the commonly used branch coverage. The required termination coverages of the subject programs are listed in Table 2. In our experiment, we calculated the infeasible paths of each program before beginning our test [32]. Further, the termination coverage is the maximum reachable coverage excluding infeasible paths.
| Program | tcas.c | print_tokens.c | print_tokens2.c | tot_info.c | schedule.c | schedule2.c | replace.c` |
|---|---|---|---|---|---|---|---|
| Termination coverage | 0.98 | 0.83 | 0.94 | 0.88 | 0.96 | 0.92 | 0.95 |
Required termination coverage of each program.
In contrast, different mutation factors have a scant effect because for DE-R, OVD-R, and DDE-R, the evolution iterations are obviously not different. This means that changing the mutation factor has almost no effect on the experiment and the key role is only adding the optimized rebirth strategy.
6.1. Analysis of Termination Evolution Times
Figure 8 compares the average evolution times of the four algorithms for the seven programs. The detailed statistics of evolution iterations are listed in Table 3.
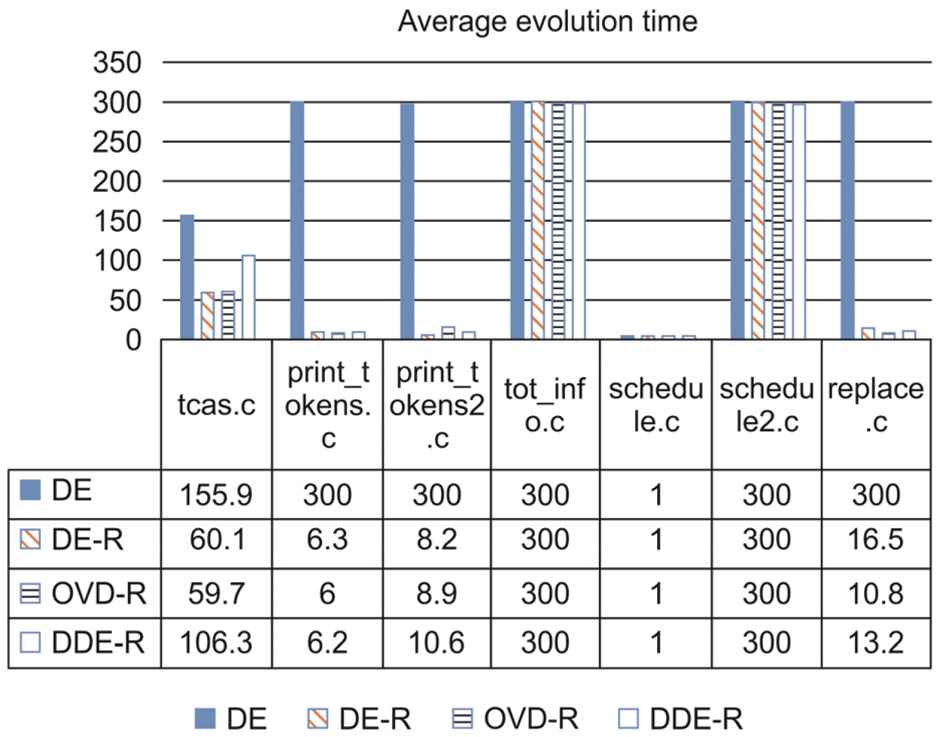
Comparison of the average evolution times: The average evolution time represents the average generations of 10 evolutions that algorithms reached the required coverage or the maximum termination iterations.
| Program | Algorithm | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | STDEV |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Differential evolution (DE) | 60 | 298 | 66 | 109 | 209 | 300 | 85 | 8 | 124 | 300 | 155.9 | 111.52 | |
| Differential evolution algorithm (DE-R) | 33 | 108 | 14 | 128 | 14 | 58 | 16 | 137 | 63 | 30 | 60.1 | 47.92 | |
| tcas.c | Optimal vector differential evolution algorithm (OVD-R) | 42 | 42 | 35 | 15 | 73 | 31 | 222 | 41 | 71 | 25 | 59.7 | 59.87 |
| Double differential evolution algorithm (DDE-R) | 28 | 300 | 123 | 97 | 118 | 85 | 57 | 85 | 63 | 107 | 106.3 | 74.06 | |
| DE | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE-R | 5 | 6 | 5 | 6 | 6 | 6 | 8 | 5 | 10 | 5 | 6.2 | 1.62 | |
| print_tokens.c | OVD-R | 40 | 4 | 5 | 10 | 5 | 5 | 5 | 4 | 4 | 7 | 8.9 | 11.08 |
| DDE-R | 9 | 7 | 10 | 6 | 7 | 5 | 5 | 7 | 6 | 5 | 6.7 | 1.70 | |
| DE | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE-R | 10 | 8 | 9 | 6 | 13 | 9 | 8 | 9 | 5 | 5 | 8.2 | 2.44 | |
| print_tokens2.c | OVD-R | 14 | 5 | 10 | 8 | 7 | 10 | 11 | 6 | 9 | 9 | 8.9 | 2.60 |
| DDE-R | 6 | 14 | 34 | 6 | 8 | 9 | 8 | 9 | 8 | 4 | 10.6 | 8.63 | |
| DE | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| tot_info.c | OVD-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 |
| DDE-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| DE-R | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| schedule.c | OVD-R | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| DDE-R | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| DE | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| schedule2.c | OVD-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 |
| DDE-R | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 | |
| DE-R | 13 | 14 | 26 | 23 | 6 | 21 | 25 | 12 | 11 | 14 | 16.5 | 6.75 | |
| replace.c | OVD-R | 14 | 6 | 13 | 9 | 8 | 17 | 1 | 13 | 15 | 12 | 10.8 | 4.80 |
| DDE-R | 25 | 18 | 10 | 8 | 16 | 19 | 5 | 18 | 9 | 4 | 13.2 | 6.94 |
Statistics of evolution iterations.
The average evolution times in Figure 8 show that, for tcas.c, print_tokens.c, print_tokens2.c, and replace.c, DE-R, OVD-R, and DDE-R can reach the required termination coverage more rapidly than DE. In particular, for print_tokens.c and print_token2.c, the evolution iterations can be greatly reduced by almost 98%. The optimization effect is obvious.
From Table 3, we can see that, in terms of the average evolution iterations, the three improved DE algorithms both have more effective evolutions than the classic DE algorithm with fewer iterations for more coverage, which means the evolution times are faster.
In contrast, different mutation factors have minimal effect because, for DE-R, OVD-R, and DDE-R, the evolution iterations are obviously not different. This means that changing the mutation factor has almost no effect on the experiment and the key role is adding the optimized rebirth strategy.
6.2. Analysis of the Final Obtained Coverage
Figure 9 shows the comparison of the finally obtained average termination coverage of the four algorithms for the seven programs.
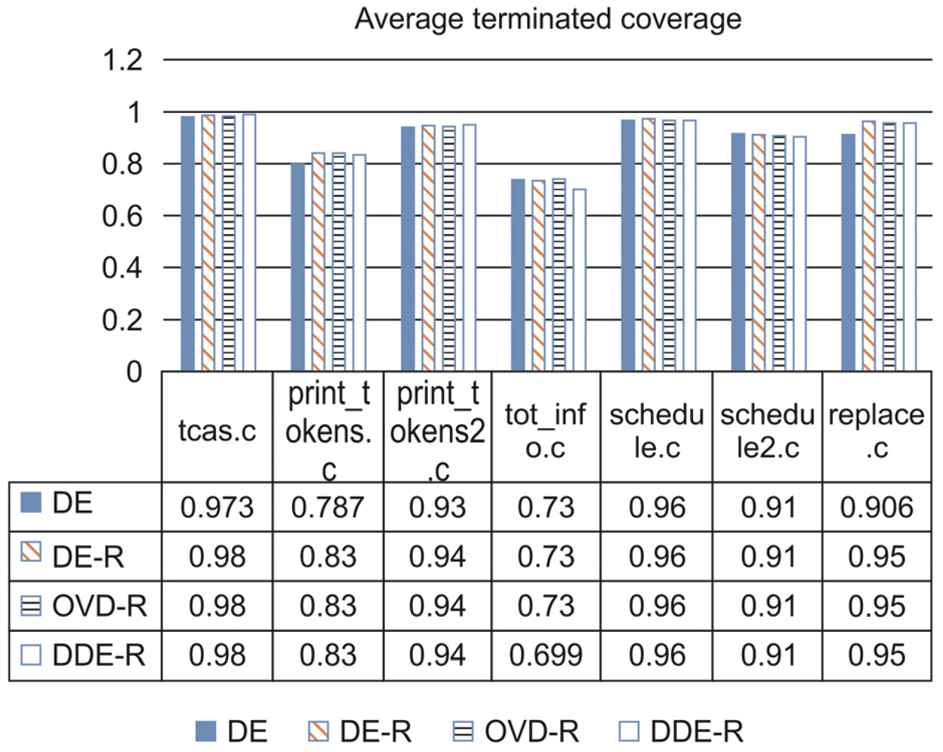
Comparison of average obtained coverage: The average terminated coverage represents the average coverage of 10 evolutions that algorithms reached the required coverage or the maximum termination iterations.
In terms of the termination coverage, as we imagined at the beginning of the experiment, the three improved DE algorithms can all reach the required termination coverage, which is better than or the same as the classic DE algorithm in most conditions except DDE-R for tot_info.c. However, the difference is not very large, and thus, not overly distinct. After carefully observing the three optimized algorithms, we find that the termination coverages they reach are in fact nearly the same. This means that different mutation factors (i.e., DE/rand/1/bin, DE/best/1/bin, and DE/rand/ 2) have minimal effect on the experiment results; and the key role of improving the experiment is adding the optimized rebirth strategy.
From the standard deviation in Table 4, we can observe that the final obtained coverages of the three improved algorithms are more stable than that of the traditional DE algorithm in most conditions except for program tot_info.c. For tot_info.c, the final obtained termination coverage of the DDE-R has a relative larger standard deviation, and the first test of DDE-R reaches 0.78, whereas others only reach 0.69. This result may have been generated by the inherent randomness of the heuristic algorithm.
| Program | Algorithm | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | STDEV |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Differential evolution (DE) | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.92 | 0.98 | 0.98 | 0.98 | 0.97 | 0.973 | 0.019 | |
| Differential evolution algorithm (DE-R) | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0 | |
| tcas.c | Optimal vector differential evolution algorithm (OVD-R) | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0 |
| Double differential evolution algorithm (DDE-R) | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0 | |
| DE | 0.8 | 0.78 | 0.79 | 0.78 | 0.78 | 0.81 | 0.79 | 0.78 | 0.78 | 0.78 | 0.787 | 0.010 | |
| DE-R | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0 | |
| print_tokens.c | OVD-R | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0 |
| DDE-R | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0 | |
| DE | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0 | |
| DE-R | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0 | |
| print_tokens2.c | OVD-R | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0 |
| DDE-R | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0 | |
| DE | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0 | |
| DE-R | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0 | |
| tot_info.c | OVD-R | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0 |
| DDE-R | 0.78 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 | 0.699 | 0.028 | |
| DE | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0 | |
| DE-R | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0 | |
| schedule.c | OVD-R | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0 |
| DDE-R | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0 | |
| DE | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 | |
| DE-R | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 | |
| schedule2.c | OVD-R | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 |
| DDE-R | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 | |
| DE | 0.91 | 0.9 | 0.9 | 0.91 | 0.91 | 0.9 | 0.91 | 0.91 | 0.91 | 0.9 | 0.906 | 0.005 | |
| DE-R | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0 | |
| replace.c | OVD-R | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0 |
| DDE-R | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0 |
Statistics of obtained coverage.
6.3. Discussion of Results
In the experiment, we found that using the classic DE software testing usually required more tests and could almost never satisfy the requirements of the termination coverage. The experiment showed that adding the rebirth strategy into the DE algorithm significantly improved the effectiveness of generating test cases. Most tests for the programs reached the required termination coverage with less evolution time. Even if the tests did not reach the required termination coverage in the termination generation, we could obtain a test case set with a higher coverage. For tcas.c, print_tokens.c, print_tokens2.c, and replace.c, the three optimized algorithms all reduced the evolution times significantly and increased the coverage to some extent. Among them, for print_tokens.c, the percentage for reducing evolution time was nearly 97%, which is a significant effect, even though the coverage increase was not so obvious. More importantly, through statistical analysis, we found that this optimization was relatively stable for both the evolution time and final obtained coverage.
Additionally, for each program under testing, the convergences of the 300th generation were the same when we used the four different algorithms, which was mostly due to the programs themselves. For example, for tot_info.c and schedule2.c, the four algorithms all ran the required generation without reaching the required termination coverage, which was particularly obvious in schedule2.c. Each of the four algorithms was tested 10 times in the schedule2.c program. The coverage of the four algorithms all reached 91% in the first generation and were still 91% in the 300th generation. None reached the required termination coverage of 92%. We conjecture this phenomenon may have occurred because of the complex code logic (but not the cyclomatic complexity), and made some statements difficult to be reached. That is, although these DE algorithms improved the software testing efficiently, there still existed some special unknown corner conditions that could not be covered, which will be our future research effort.
7. CONCLUSIONS
In order to improve the effectiveness of the DE algorithm for more effective software testing, we developed an optimized strategy. When the aging parameter is more than the threshold, the rebirth operation will be triggered automatically to form a new evolution process with partial memory embodied by the accumulated coverage. This simple rebirth strategy with part memory as the fitness function can be easily added to traditional DE algorithms with different mutation strategies and form three new optimized DE algorithms. We selected the seven programs from the Siemens program set as the subject programs for testing. By constructing the automatic executing testing platform and completing the required tests, we verified the feasibility of all three improved algorithms by adopting the proposed strategy. The results also showed that, in most conditions, the optimized DE algorithms significantly increased the effectiveness of testing for the required termination coverage with less evolution time and fewer test cases.
ACKNOWLEDGMENTS
This study is supported by the NSFC (61672080) and National Aerospace Science Foundation of China (2011ZD51055 and 2016ZD51031). We would like to thank Editage [www.editage.cn] for English language editing.
REFERENCES
Cite this article
TY - JOUR AU - Xiaodong Gou AU - Tingting Huang AU - Shunkun Yang AU - Mengxuan Su AU - Fuping Zeng PY - 2018 DA - 2018/11/19 TI - Optimized Differential Evolution Algorithm for Software Testing JO - International Journal of Computational Intelligence Systems SP - 215 EP - 226 VL - 12 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.2018.125905642 DO - 10.2991/ijcis.2018.125905642 ID - Gou2018 ER -
